考点:直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:方法一、在平面AA1B1B内,作MK∥AB,交BB1于K点,连接KN,利用“面面平行”⇒“线面平行”即可.
方法二、连接BM,延长交A1B1于L,连接C1L,运用平行线分线段成比例的逆定理,证得MN∥C1L,由线面平行的判定定理,即可得证;
方法三、分别在平面AB1,和平面BC1中,过M作MH∥BB1,过N作NG∥BB1,运用平行线分线段成比例,证得四边形MNGH为平行四边形,再由线面平行的判定定理,即可得证.
解答:
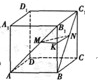
证法一:在平面AA
1B
1B内,作MK∥AB,交BB
1于K点,连接KN,
则易知
=
;
∵
=
,
∴
=
,
∴KN∥B
1C
1,又A
1B
1∥AB,∴MK∥A
1B
1.
∴平面MKN∥平面A
1B
1C
1D
1,而MN?平面MKN,
∴MN∥平面A
1B
1C
1D
1.
证法二:连接BM,延长交A
1B
1于L,连接C
1L,

则
=
,又
=
,
则
=
,即有MN∥C
1L,
MN?平面A
1B
1C
1D
1.C
1L?平面A
1B
1C
1D
1.
则MN∥平面A
1B
1C
1D
1.
证法三、分别在平面AB
1,和平面BC
1中,
过M作MH∥BB
1,过N作NG∥BB
1,
则MH∥NG,由于
===,
即有MH=NG,则四边形MNGH为平行四边形,
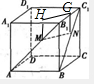
则有MN∥GH,MN?平面A
1B
1C
1D
1.GH?平面A
1B
1C
1D
1.
则有MN∥平面A
1B
1C
1D
1.
点评:本题考查直线与平面平行的判定,考查作辅助线进行推理证明的能力,属于中档题.

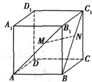 如图,在正方体ABCD-A1B1C1D1中,M、N分别是对角线AB1、BC1上的点,且
如图,在正方体ABCD-A1B1C1D1中,M、N分别是对角线AB1、BC1上的点,且 证法一:在平面AA1B1B内,作MK∥AB,交BB1于K点,连接KN,
证法一:在平面AA1B1B内,作MK∥AB,交BB1于K点,连接KN,



 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 为了丰富学生的课余生活,增加学生的阅读面,亳州一中南校计划在综合楼建造一个室内面积为800平方米的矩形电子阅览室,在阅览室内沿左右两侧与后墙内侧各保留1m宽的通道,沿前侧内墙保留3m的空地,当矩形阅览室边长各为多少时,面积最大,最大为多少?
为了丰富学生的课余生活,增加学生的阅读面,亳州一中南校计划在综合楼建造一个室内面积为800平方米的矩形电子阅览室,在阅览室内沿左右两侧与后墙内侧各保留1m宽的通道,沿前侧内墙保留3m的空地,当矩形阅览室边长各为多少时,面积最大,最大为多少?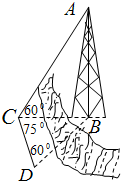 测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得∠BCD=75°,∠BDC=60°,CD=100m.并在点C测得塔顶A的仰角∠ACB=60°,求:塔高AB.
测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得∠BCD=75°,∠BDC=60°,CD=100m.并在点C测得塔顶A的仰角∠ACB=60°,求:塔高AB.