
分析 (1)设直线l的方程为:y=kx+m,联立$\left\{\begin{array}{l}{y=kx+m}\\{3{x}^{2}+4{y}^{2}=12λ}\end{array}\right.$,得:(3+4k2)x2+8kmx+4(m2-3λ)=0,由此根的判别式、韦达定理、等比数列可得k的值;
(2)求得判别式大于0的情况,运用点到直线的距离公式和弦长公式,运用三角形的面积公式,由条件解出λ=$\frac{2{m}^{2}}{3}$+$\frac{1}{2{m}^{2}}$+1,运用基本不等式即可得到最小值及对应的m的值.
解答 解:(1)由题意可设直线l的方程为:y=kx+m(k>0,m≠0),
联立$\left\{\begin{array}{l}{y=kx+m}\\{3{x}^{2}+4{y}^{2}=12λ}\end{array}\right.$,消去y并整理,得:(3+4k2)x2+8kmx+4(m2-3λ)=0,
则△=64k2m2-16(3+4k2)(m2-3λ)=16(4λk2-m2+3λ)>0,
此时设M(x1,y1)、N(x2,y2),
则x1+x2=-$\frac{8km}{3+4{k}^{2}}$,x1x2=$\frac{4({m}^{2}-3λ)}{3+4{k}^{2}}$,
于是y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2,
又直线OM、MN、ON的斜率依次成等比数列,
∴$\frac{{y}_{1}}{{x}_{1}}$•$\frac{{y}_{2}}{{x}_{2}}$=$\frac{{k}^{2}{x}_{1}{x}_{2}+km({x}_{1}+{x}_{2})+{m}^{2}}{{x}_{1}{x}_{2}}$=k2,
∴-$\frac{8{k}^{2}{m}^{2}}{3+4{k}^{2}}$+m2=0,
由m≠0得:k2=$\frac{3}{4}$,解得k=$\frac{\sqrt{3}}{2}$(负的舍去);
(2)由△>0 得:λ>$\frac{1}{6}$m2,
设原点O到直线l的距离为d,
则S△OMN=$\frac{1}{2}$|MN|d=$\frac{1}{2}$•$\frac{|m|}{\sqrt{1+{k}^{2}}}$•$\sqrt{1+{k}^{2}}$|x1-x2|
=$\frac{1}{2}$|m|$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{1}{2}$|m|•$\sqrt{\frac{64{k}^{2}{m}^{2}}{(3+4{k}^{2})^{2}}-\frac{16{m}^{2}-48λ}{3+4{k}^{2}}}$=m2+1,
由4k2=3,代入化简可得λ=$\frac{2{m}^{2}}{3}$+$\frac{1}{2{m}^{2}}$+1≥2$\sqrt{\frac{2{m}^{2}}{3}•\frac{1}{2{m}^{2}}}$+1=$\frac{2\sqrt{3}}{3}$+1.
当且仅当$\frac{2{m}^{2}}{3}$=$\frac{1}{2{m}^{2}}$,即m=±$\sqrt{\frac{\sqrt{3}}{2}}$时,λ的最小值为$\frac{2\sqrt{3}}{3}$+1.
点评 本题考查椭圆方程的运用,考查三角形面积的求法,解题时要注意根的判别式、韦达定理、等比数列、弦长公式、基本不等式等知识点的灵活运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{7}$,+∞) | B. | [$\frac{1}{7}$,$\frac{1}{3}$) | C. | (-∞,$\frac{1}{3}$) | D. | (-∞,$\frac{1}{7}$]∪($\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
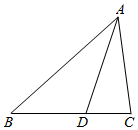 如图,在△ABC中,记$\overrightarrow{BA}=\overrightarrow a,\overrightarrow{BC}=\overrightarrow b$,∠B=$\frac{π}{3}$,AB=8,点D在BC边上,且CD=2,cos∠ADC=$\frac{1}{7}$.
如图,在△ABC中,记$\overrightarrow{BA}=\overrightarrow a,\overrightarrow{BC}=\overrightarrow b$,∠B=$\frac{π}{3}$,AB=8,点D在BC边上,且CD=2,cos∠ADC=$\frac{1}{7}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com