
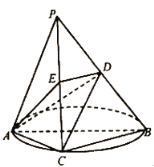
【题目】如图,![]() 是一个三棱锥,
是一个三棱锥,![]() 是圆的直径,
是圆的直径,![]() 是圆上的点,
是圆上的点,![]() 垂直圆所在的平面,
垂直圆所在的平面,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)若二面角![]() 是
是![]() ,
,![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)可证![]() ,
,![]() ,再利用
,再利用![]() 可得
可得![]() ,
,![]() ,从而可证
,从而可证![]() 平面
平面![]() .
.
(2)可证![]() 为二面角
为二面角![]() 的平面角,再以
的平面角,再以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 方向分别为
方向分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向,建立如图所示的空间直角坐标系
轴的正方向,建立如图所示的空间直角坐标系![]() . 求出平面
. 求出平面![]() 的法向量和直线
的法向量和直线![]() 的方向向量后可求
的方向向量后可求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)因为![]() 是圆的直径,所以
是圆的直径,所以![]() .
.
因为![]() 垂直圆所在的平面,且
垂直圆所在的平面,且![]() 在该平面中,所以
在该平面中,所以![]() .
.
因为![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,
的中点,
所以![]() ,所以
,所以![]() ,
,![]()
又因为![]() ,所以有
,所以有![]() 平面
平面![]() .
.
(2)由(1)可知,![]() ,
,![]() ,
,
所以![]() 为二面角
为二面角![]() 的平面角,
的平面角,
从而有![]() ,则
,则![]() .
.
又![]() ,
,![]() ,得
,得![]() .
.
以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 方向分别为
方向分别为![]() 轴,
轴,![]() 轴,
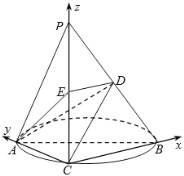
轴,![]() 轴的正方向,建立如图所示的空间直角坐标系
轴的正方向,建立如图所示的空间直角坐标系![]() .
.
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则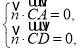
即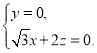 可取
可取![]() .
.
故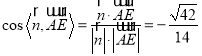 .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为了了解居民的家庭收人情况,某社区组织工作人员从该社区的居民中随机抽取了![]() 户家庭进行问卷调查.经调查发现,这些家庭的月收人在
户家庭进行问卷调查.经调查发现,这些家庭的月收人在![]() 元到
元到![]() 元之间,根据统计数据作出如图所示的频率分布直方图.已知图中从左至右第一 、二、四小组的频率之比为
元之间,根据统计数据作出如图所示的频率分布直方图.已知图中从左至右第一 、二、四小组的频率之比为![]() ,且第四小组的频数为
,且第四小组的频数为![]() .
.
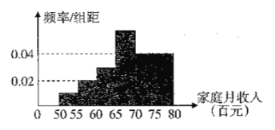
(1)求![]() ;
;
(2)求这![]() 户家庭月收人的众数与中位数(结果精确到
户家庭月收人的众数与中位数(结果精确到![]() );
);
(3)这![]() 户家庭月收入在第一、二、三小组的家庭中,用分层抽样的方法任意抽取
户家庭月收入在第一、二、三小组的家庭中,用分层抽样的方法任意抽取![]() 户家庭,并从这
户家庭,并从这![]() 户家庭中随机抽取
户家庭中随机抽取![]() 户家庭进行慰问,求这
户家庭进行慰问,求这![]() 户家庭月收入都不超过
户家庭月收入都不超过![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款应用软件,为激发大家的学习兴趣,他们推出了“解数学题获取软件激活码”的活动,这款软件的激活码为下列数学问题的答案:已知数列1、1、2、1、2、4、8、1、2、4、8、16、……,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,再接下来的三项是
,再接下来的三项是![]() ,……,以此类推,求满足如下条件的最小整数
,……,以此类推,求满足如下条件的最小整数![]() 且该数列的前
且该数列的前![]() 项和为2的整数幂,那么该软件的激活码是________。
项和为2的整数幂,那么该软件的激活码是________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形![]() 为正方形,
为正方形,![]() 平面
平面![]() ,四边形
,四边形![]() 与四边形
与四边形![]() 也都为正方形,连接
也都为正方形,连接![]() ,点
,点![]() 为
为![]() 的中点,有下述四个结论:
的中点,有下述四个结论:
①![]() ; ②
; ②![]() 与
与![]() 所成角为
所成角为![]() ;
;
③![]() 平面
平面![]() ; ④
; ④![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
其中所有正确结论的编号是( )
A.①②B.①②③C.①③④D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业团队拟生产![]() 两种产品,根据市场预测,
两种产品,根据市场预测,![]() 产品的利润与投资额成正比(如图1),
产品的利润与投资额成正比(如图1),![]() 产品的利润与投资额的算术平方根成正比(如图2).(注: 利润与投资额的单位均为万元)
产品的利润与投资额的算术平方根成正比(如图2).(注: 利润与投资额的单位均为万元)

(注:利润与投资额的单位均为万元)
(1)分別将![]() 两种产品的利润
两种产品的利润![]() 、
、![]() 表示为投资额
表示为投资额![]() 的函数;
的函数;
(2)该团队已筹集到10 万元资金,并打算全部投入![]() 两种产品的生产,问:当
两种产品的生产,问:当![]() 产品的投资额为多少万元时,生产
产品的投资额为多少万元时,生产![]() 两种产品能获得最大利润,最大利润为多少?
两种产品能获得最大利润,最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 过点
过点![]() ,
,![]() 为其焦点,过
为其焦点,过![]() 且不垂直于
且不垂直于![]() 轴的直线
轴的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,动点
两点,动点![]() 满足
满足![]() 的垂心为原点
的垂心为原点![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)求证:动点![]() 在定直线
在定直线![]() 上,并求
上,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
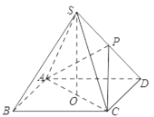
【题目】如图,在四棱锥![]() 中,已知四边形
中,已知四边形![]() 是边长为
是边长为![]() 的正方形,点
的正方形,点![]() 在底面
在底面![]() 上的射影为底面
上的射影为底面![]() 的中心点
的中心点![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() 的面积为1.
的面积为1.
(1)若点![]() 是
是![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在一点
上是否存在一点![]() 使得二面角
使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com