
分析 由条件利用同角三角函数的基本关系求得sin(θ+$\frac{π}{3}$)的值,再利用两角差的正弦公式求得要求式子的值.
解答 解:∵θ为第二象限角,若$tan(θ+\frac{π}{3})=\frac{1}{2}$>0,∴θ+$\frac{π}{3}$为第三象限角,
由$\frac{sin(θ+\frac{π}{3})}{cos(θ+\frac{π}{3})}$=$\frac{1}{2}$,sin(θ+$\frac{π}{3}$)<0,cos(θ+$\frac{π}{3}$)<0,${sin}^{2}(θ+\frac{π}{3})$+${cos}^{2}(θ+\frac{π}{3})$=1,
求得sin(θ+$\frac{π}{3}$)=-$\frac{\sqrt{5}}{5}$,
则sinθ+$\sqrt{3}$cosθ=2sin(θ+$\frac{π}{3}$)=-$\frac{2\sqrt{5}}{5}$,
故答案为:-$\frac{2\sqrt{5}}{5}$.
点评 本题主要考查同角三角函数的基本关系,两角差的正弦公式的应用,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$+1 | B. | 2 | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,$\frac{2}{3}$] | B. | [-$\frac{1}{3}$,2) | C. | (-∞,$\frac{2}{3}$] | D. | [-$\frac{2}{3}$,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
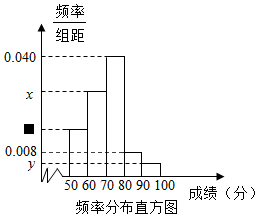 某中学为了解某次竞赛成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题:
某中学为了解某次竞赛成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图解决下列问题:| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 9 | 0.18 |
| 第2组 | [60,70) | a | ▓ |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) | ▓ | 0.08 |
| 第5组 | [90,100] | 2 | b |
| 合计 | ▓ | ▓ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com