Question

4．如图，公园有一块边长为2的等边三角形△ABC的地，现修成草坪，图中DE把草坪分成面积相等的两部分，D在AB上，E在AC上．
（1）设AD=x，DE=y，请将y表示为x的函数，并求出该函数的定义域；
（2）如果DE是灌溉水管，为节约成本，希望它最短，DE的位置应在哪里？如果DE是参观线路，则希望它最长，DE的位置又应在哪里？请予以说明．

Answer 1

分析 （1）利用三角形的面积公式得出AE与x的关系，再使用余弦定理得出y关于x的函数；
（2）利用基本不等式求y的最小值，利用函数单调性求y的最大值．

解答 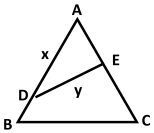解：（1）在△ADE中，由余弦定理得：y²=x²+AE²-2x•AE•cos60°，
∴y²=x²+AE²-x•AE，①
又S_△ADE=$\frac{1}{2}$AE•x•sin60°=$\frac{1}{2}$S_△ABC=$\frac{\sqrt{3}}{2}$，∴x•AE=2，即AE=$\frac{2}{x}$，
∴${y^2}={x^2}+{（\frac{2}{x}）^2}-2$（y＞0），
∴$y=\sqrt{{x^2}+\frac{4}{x^2}-2}$．x∈[1，2]．
（2）如果DE是水管，$y=\sqrt{{x^2}+\frac{4}{x^2}-2}≥\sqrt{2•2-2}=\sqrt{2}$
当且仅当${x^2}=\frac{4}{x^2}$，即$x=\sqrt{2}$时等号成立，
此时AD=DE=AE=$\sqrt{2}$．
如果DE是参观线路，记$f（x）={x^2}+\frac{4}{x^2}$-2，
则f（x）在$[1，\sqrt{2}]$上递减，在$[\sqrt{2}，2]$上递增，
且f（1）=f（2）=3，
∴y_max=$\sqrt{3}$，此时DE为AB边的中线或AC边的中线．

点评 本题考查了函数最值的解法，函数单调性与基本不等式的应用，属于中档题．