
分析 (Ⅰ)求出函数的导数,问题转化为a≥$\frac{1}{x}$在[1,+∞)上恒成立,求出a的最小值即可;
(Ⅱ)求出m(x)=min{xlnx,$\frac{x}{{e}^{x}}$},当0<x≤1时,xf(x)=xlnx≤0,而$\frac{1}{g(x)}$=$\frac{x}{{e}^{x}}$>0,故此时有xf(x)<$\frac{1}{g(x)}$,设F(x)=xlnx-$\frac{x}{{e}^{x}}$,根据函数的单调性证明即可.
解答 解:(Ⅰ)∵函数g(x)=$\frac{{e}^{ax}}{x}$在[1,+∞)上是增函数.
∴g′(x)=$\frac{{(ax-1)e}^{ax}}{{x}^{2}}$≥0在[1,+∞)上恒成立,
即ax-1≥0在[1,+∞)上恒成立,
即a≥$\frac{1}{x}$在[1,+∞)上恒成立,
即a≥1,故实数a的最小值为1;
证明:(Ⅱ)由已知可得:G(x)=ex
若x0是f(x)=lnx=$\frac{1}{G(x)}$=e-x的根且x0∈(1,2),
当a=1时,g(x)=$\frac{{e}^{x}}{x}$,$\frac{1}{g(x)}$=xe-x,
m(x)=min{xlnx,$\frac{x}{{e}^{x}}$},
当0<x≤1时,xf(x)=xlnx≤0,
而$\frac{1}{g(x)}$=$\frac{x}{{e}^{x}}$>0,
故此时有xf(x)<$\frac{1}{g(x)}$,
设F(x)=xlnx-$\frac{x}{{e}^{x}}$,
∵F′(x)=1+lnx+$\frac{x-1}{{e}^{x}}$,
x>1时,F′(x)>0,且存在x0∈(1,2),
使得F(x0)=x0lnx0-$\frac{{x}_{0}}{{e}^{{x}_{0}}}$=$\frac{{x}_{0}{(e}^{{x}_{0}}l{nx}_{0}-1)}{{e}^{{x}_{0}}}$=0,
故1<x<x0时,xf(x)<$\frac{1}{g(x)}$,
当x>x0时,xf(x)>$\frac{1}{g(x)}$,
∴m(x)=$\left\{\begin{array}{l}{xlnx,0<x{≤x}_{0}}\\{\frac{x}{{e}^{x}},x{>x}_{0}}\end{array}\right.$,
显然当1<x<x0时,m(x)=xlnx,m′(x)=1+lnx>0,m(x)递增,
当x>x0时,m(x)=$\frac{x}{{e}^{x}}$,m′(x)=$\frac{1-x}{{e}^{x}}$<0,m(x)递减,
由m(x)=n在(1,+∞)上有2个不等实根x1,x2,(x1<x2),
知x1∈(1,x0),x2∈(x0,+∞),
显然当x2→+∞时,x1+x2>2x0,
下面用分析法证明:
要证x1+x2>2x0,即证x2>2x0-x1>x0,
而m(x)在(x0,+∞)递减,
故可证m(x2)<m(2x0-x1),
又m(x1)=m(x2),即证m(x1)<m(2x0-x1),即x1lnx1<$\frac{{2x}_{0}{-x}_{1}}{{e}^{{2x}_{0}{-x}_{1}}}$,
记h(x)=xlnx-$\frac{{2x}_{0}-x}{{e}^{{2x}_{0}-x}}$,1<x<x0,其中h(x0)=0,
h′(x)=1+lnx+$\frac{1+x-{2x}_{0}}{{e}^{{2x}_{0}-x}}$=1+lnx+$\frac{1}{{e}^{{2x}_{0}-x}}$-$\frac{{2x}_{0}-x}{{e}^{{2x}_{0}-x}}$,
记ω(t)=$\frac{t}{{e}^{t}}$,ω′(t)=$\frac{1-t}{{e}^{t}}$,
当t∈(0,1)时,ω′(t)>0,t∈(1,+∞)时,ω′(t)<0,
故ω(t)max=$\frac{1}{e}$,
而ω(t)>0,故0<ω(t)<$\frac{1}{e}$,
而2x0-x>0,
从而-$\frac{1}{e}$<-$\frac{{2x}_{0}-x}{{e}^{{2x}_{0}-x}}$<0,
因此h′(x)>1-$\frac{1}{e}$>0,即h(x)递增,
从而1<x<x0时,h(x)<h(x0)=0,
即x1lnx1<$\frac{2{{x}_{0}-x}_{1}}{{e}^{{2x}_{0}{-x}_{1}}}$,
故x1+x2>2x0,得证.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,考查不等式的证明以及转化思想,是一道综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
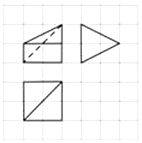
| A. | $10+\sqrt{5}$ | B. | $7+3\sqrt{5}$ | C. | $8+\sqrt{5}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在正方体ABCD-A1B1C1D1中,棱AB的中点为P,若光线从点P出发,依次经三个侧面BCC1B1,DCC1D1,ADD1A1反射后,落到侧面ABB1A1(不包括边界),则入射光线PQ与侧面BCC1B1所成角的正切值的范围是( )
如图,在正方体ABCD-A1B1C1D1中,棱AB的中点为P,若光线从点P出发,依次经三个侧面BCC1B1,DCC1D1,ADD1A1反射后,落到侧面ABB1A1(不包括边界),则入射光线PQ与侧面BCC1B1所成角的正切值的范围是( )| A. | ($\frac{3}{4}$,$\frac{5}{4}$) | B. | ($\frac{2\sqrt{17}}{17}$,4) | C. | ($\frac{\sqrt{5}}{5}$,$\frac{3}{2}$) | D. | ($\frac{3\sqrt{5}}{10}$,$\frac{5}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
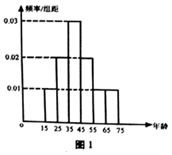 持续性的雾霾天气严重威胁着人们的身体健康,汽车的尾气排放是造成雾霾天气的重要因素之一.为此,某城市实施了机动车尾号限行,该市报社调查组为了解市区公众对“车辆限行”的态度,随机选取了30人进行调查,将他们的年龄(单位:岁)数据绘制成频率分布直方图(图1),并将调查情况进行整理后制成表2:
持续性的雾霾天气严重威胁着人们的身体健康,汽车的尾气排放是造成雾霾天气的重要因素之一.为此,某城市实施了机动车尾号限行,该市报社调查组为了解市区公众对“车辆限行”的态度,随机选取了30人进行调查,将他们的年龄(单位:岁)数据绘制成频率分布直方图(图1),并将调查情况进行整理后制成表2:| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 3 | 6 | 6 | 3 | ||
| 赞成人数 | 2 | 4 | 5 | 4 | 2 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com