
分析 (1)由题意可得:a=2,b=c,a2+b2=c2,解出即可得出.
(2)设P(x0,y0),若过点P的切线斜率都存在,设其方程为y-y0=k(x-x0),与椭圆方程联立化为:$(1+2{k^2}){x^2}+4k({y_0}-k{x_0})x+2{(k{x_0}-{y_0})^2}-4=0$,
根据直线与椭圆相切,可得△=0,利用根与系数的关系、相互垂直的直线斜率之间的关系即可得出.若过点P的切线有一条斜率不存在,容易得出.
解答 解:(1)a=2,b=c,a2+b2=c2,
∴b2=2,
∴椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{2}=1$.
(2)设P(x0,y0),若过点P的切线斜率都存在,设其方程为y-y0=k(x-x0),
由$\left\{{\begin{array}{l}{y-{y_0}=k(x-{x_0})}\\{{x^2}+2{y^2}=4}\end{array}}\right.$得,$(1+2{k^2}){x^2}+4k({y_0}-k{x_0})x+2{(k{x_0}-{y_0})^2}-4=0$,
∵直线与椭圆相切,∴△=0,${[4k({y_0}-k{x_0})]^2}-4(1+2{k^2})[2{(k{x_0}-{y_0})^2}-4]=0$,
整理得$(4-x_0^2){k^2}+2{x_0}{y_0}k+2-y_0^2=0$,
∵椭圆C的两条切线的斜率分别为k1,k2,由韦达定理,${k_1}•{k_2}=\frac{2-y_0^2}{4-x_0^2}$,
∵点P在圆O上,∴$x_0^2+y_0^2=6$,即$y_0^2=6-x_0^2$,
∴${k_1}•{k_2}=\frac{2-y_0^2}{4-x_0^2}=\frac{2-(6-x_0^2)}{4-x_0^2}=\frac{-4+x_0^2}{4-x_0^2}=-1$,
∴l1⊥l2,
特别的,若过点P的切线有一条斜率不存在,不妨设该直线为l1,
则l1的方程为x=±2,l2的方程为$y=±\sqrt{2}$,∴l1⊥l2,
综上,对任意满足题设的点P,都有l1⊥l2.
点评 本题考查了椭圆的标准方程及其性质、一元二次方程的根与系数的关系、直线与椭圆相切的性质、中点坐标公式、线段垂直平分线的性质,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
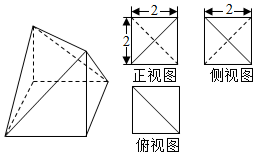 已知某几何体的直观图及三视图如图所示,三视图的轮廓均为正方形,则该几何体的表面积为( )
已知某几何体的直观图及三视图如图所示,三视图的轮廓均为正方形,则该几何体的表面积为( )| A. | 14+2$\sqrt{3}$ | B. | 12+4$\sqrt{3}$ | C. | 16+4$\sqrt{3}$ | D. | 15+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,正方体ABCD-A1B1C1D1中,E为线段B1C的中点,若三棱锥E-ADD1外接球的体积为36π,则正方体的棱长为( )
如图,正方体ABCD-A1B1C1D1中,E为线段B1C的中点,若三棱锥E-ADD1外接球的体积为36π,则正方体的棱长为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3] | B. | [-1,8] | C. | (0,6] | D. | [2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在点x=x0处的斜率 | |
| B. | 在点 ( x0,f ( x0 ) ) 处的切线与x轴所夹的锐角正切值 | |
| C. | 点 ( x0,f ( x0 ) ) 与点 (0,0 ) 连线的斜率 | |
| D. | 曲线y=f(x)在点 ( x0,f ( x0 ) ) 处的切线的斜率. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2)∪(1,3) | B. | (-3,-1)∪(1,2) | C. | (-2,3)∪(-1,1) | D. | (-3,1)∪(-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com