
| A. | (-2,2)∪(1,3) | B. | (-3,-1)∪(1,2) | C. | (-2,3)∪(-1,1) | D. | (-3,1)∪(-1,2) |
分析 关于x的不等式$\frac{kx}{ax+1}+\frac{bx+1}{cx+1}<0$可看成前者不等式中的x用$\frac{1}{x}$代入可得不等式$\frac{kx}{ax+1}+\frac{bx+1}{cx+1}<0$的解集.
解答 解:若关于x的不等式$\frac{k}{x+a}+\frac{x+b}{x+c}<0$的解集为$(-1,-\frac{1}{3})∪(\frac{1}{2},1)$,
则关于x的不等式$\frac{kx}{ax+1}+\frac{bx+1}{cx+1}<0$可看成前者不等式中的x用$\frac{1}{x}$代入可得,
则$\frac{1}{x}$∈$(-1,-\frac{1}{3})∪(\frac{1}{2},1)$,则x∈(-3,-1)∪(1,2),
故选:B.
点评 本题考查不等式的解法,考查方法的类比,正确理解题意是关键.


科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{2}$,1] | B. | (0,1) | C. | (-$\frac{1}{2}$,$\frac{1}{2}$) | D. | [0,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
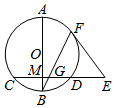 如图,AB是圆O的直径,弦CD⊥AB于点M,点E是CD延长线上一点,AB=10,CD=8,3ED=4OM,EF切圆O于F,BF交CD于点G.
如图,AB是圆O的直径,弦CD⊥AB于点M,点E是CD延长线上一点,AB=10,CD=8,3ED=4OM,EF切圆O于F,BF交CD于点G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com