
分析 (Ⅰ)先求出基本事件总数n=${C}_{7}^{4}$,利用对立事件概率计算公式能求出事件A的概率.
(Ⅱ)由题意知随机变量X的所有可能取值为0,2,4,分别求出相应的概率,由此能求出随机变量X的分布列和数学期望.
解答 解:(Ⅰ)高二年级学生会有理科生4名,其中3名男同学;文科生3名,其中有1名男同学,
从这7名成员中随机抽4人参加高中示范校验收活动问卷调查,
基本事件总数n=${C}_{7}^{4}$,
A为事件“选出的4人中既有文科生又有理科生”,
则事件A的概率p=1-$\frac{{C}_{4}^{4}}{{C}_{7}^{4}}$=$\frac{34}{35}$,
(Ⅱ)由题意知随机变量X的所有可能取值为0,2,4,
P(X=4)=$\frac{{C}_{4}^{4}{C}_{3}^{0}}{{C}_{7}^{4}}$=$\frac{1}{35}$,
P(X=2)=$\frac{{C}_{4}^{3}{C}_{3}^{1}+{C}_{4}^{1}{C}_{3}^{3}}{{C}_{7}^{4}}$=$\frac{16}{35}$,
P(X=0)=$\frac{{C}_{4}^{2}{C}_{3}^{2}}{{C}_{7}^{4}}$=$\frac{18}{35}$.
∴随机变量X的分布列为:
| X | 0 | 2 | 4 |
| P | $\frac{18}{35}$ | $\frac{16}{35}$ | $\frac{1}{35}$ |
点评 本题考查概率、离散型随机变量的分布列、数学期望等基础知识,考查推理论证能力、运算求解能力、数据处理能力,考查函数与方程思想、化归与转化思想,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
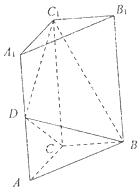 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=$\frac{1}{2}$AA1=1,D是棱AA1上的点,DC1⊥BD
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=$\frac{1}{2}$AA1=1,D是棱AA1上的点,DC1⊥BD查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-∞,-1) | C. | (-∞,-1)∪(-1,+∞) | D. | (-∞,-1),(-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com