
分析 根据“可等域区间”的定义分别进行判断即可得到结论.
解答 解:①对于f(x)=sin$\frac{π}{2}$x,存在“可等域区间”,如 x∈[0,1]时,f(x)=sin$\frac{π}{2}$x∈[0,1];
②对于函数f(x)=2x2-1,存在“可等域区间”,如 x∈[-1,1]时,f(x)=2x2-1∈[-1,1];
③对于函数f(x)=|1-2x|,存在“可等域区间”,如x∈[0,1]时,f(x)=|2x-1|∈[0,1];
④∵f(x)=log2(2x-2)单调递增,且函数的定义域为(1,+∞),
若存在“可等域区间”,则满足$\left\{\begin{array}{l}{lo{g}_{2}(2m-2)=m}\\{lo{g}_{2}(2n-2)=n}\end{array}\right.$,即$\left\{\begin{array}{l}{2m-2={2}^{m}}\\{2n-2={2}^{n}}\end{array}\right.$,
∴m,n是方程2x-2x+2=0的两个根,设f(x)=2x-2x+2,f′(x)=2xln2-2,当x>1时,f′(x)>0,此时函数f(x)单调递增,
∴f(x)=2x-2x+2=0不可能存在两个解,
故f(x)=log2(2x-2)不存在“可等域区间”.
所以其中存在“可等域区间”的“可等域函数”为①②③.
故答案为:①②③
点评 本题主要考查与函数有关的新定义问题,根据“可等域区间”的定义,建立条件关系是解决本题的关键,综合性较强,属于中档题.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
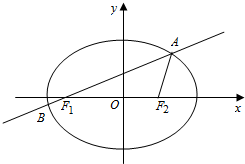 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,F1、F2为其左、右焦点,过F1的直线l交椭圆于A、B两点,△F1AF2的周长为$2(\sqrt{2}+1)$.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,F1、F2为其左、右焦点,过F1的直线l交椭圆于A、B两点,△F1AF2的周长为$2(\sqrt{2}+1)$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,△ABC是边长为2的正三角形,AE⊥平面ABC,且AE=1,又平面BCD⊥平面ABC,且BD=CD,BD⊥CD.
如图,△ABC是边长为2的正三角形,AE⊥平面ABC,且AE=1,又平面BCD⊥平面ABC,且BD=CD,BD⊥CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 6 | C. | 18 | D. | 54 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 70 | 80 |
| A. | 210 | B. | 211.5 | C. | 212 | D. | 212.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α⊥β,α∩β=m,m⊥n,则n⊥α,n⊥β | |
| B. | 若α∥β,α∩γ=m,β∩γ=n,则m∥n | |
| C. | 若m不垂直于α,则m不可能垂直于α内的无数条直线 | |
| D. | 若α∩β=m,n∥m,则n∥α,且n∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com