
分析 (1)根据余弦函数的周期定义,判断cosg(x+6π)是否等于cosg(x)即可;
(2)根据f(x)的值域为R,便可得到存在x0,使得f(x0)=c,而根据f(x)在R上单调递增即可说明x0∈[a,b],从而完成证明;
(3)只需证明u0+T为方程cosf(x)=1在区间[T,2T]上的解得出u0为方程cosf(x)=1在[0,T]上的解,是否为方程的解,带入方程,使方程成立便是方程的解.证明对任意x∈[0,T],都有f(x+T)=f(x)+f(T),可讨论x=0,x=T,x∈(0,T)三种情况:x=0时是显然成立的;x=T时,可得出cosf(2T)=1,从而得到f(2T)=2k1π,k1∈Z,根据f(x)单调递增便能得到k1>2,然后根据f(x)的单调性及方程cosf(x)=1在[T,2T]和它在[0,T]上解的个数的情况说明k1=3,和k1≥5是不存在的,而k1=4时结论成立,这便说明x=T时结论成立;而对于x∈(0,T)时,通过考查cosf(x)=c的解得到f(x+T)=f(x)+f(T),综合以上的三种情况,最后得出结论即可.
解答 解:(1)g(x)=x+sin$\frac{x}{3}$;
∴$cosg(x+6π)=cos(x+6π+sin\frac{x+6π}{3})$=$cos(x+sin\frac{x}{3})$=cosg(x)
∴g(x)是以6π为周期的余弦周期函数;
(2)∵f(x)的值域为R;
∴存在x0,使f(x0)=c;
又c∈[f(a),f(b)];
∴f(a)≤f(x0)≤f(b),而f(x)为增函数;
∴a≤x0≤b;
即存在x0∈[a,b],使f(x0)=c;
(3)证明:若u0+T为方程cosf(x)=1在区间[T,2T]上的解;
则:cosf(u0+T)=1,T≤u0+T≤2T;
∴cosf(u0)=1,且0≤u0≤T;
∴u0为方程cosf(x)=1在[0,T]上的解;
∴“u0为方程cosf(x)=1在[0,T]上得解”的充分条件是“u0+T为方程cosf(x)=1在区间[T,2T]上的解”;下面证明对任意x∈[0,T],都有f(x+T)=f(x)+f(T):
①当x=0时,f(0)=0,∴显然成立;
②当x=T时,cosf(2T)=cosf(T)=1;
∴f(2T)=2k1π,(k1∈Z),f(T)=4π,且2k1π>4π,∴k1>2;
1)若k1=3,f(2T)=6π,由(2)知存在x0∈(0,T),使f(x0)=2π;
cosf(x0+T)=cosf(x0)=1⇒f(x0+T)=2k2π,k2∈Z;
∴f(T)<f(x0+T)<f(2T);
∴4π<2k2π<6π;
∴2<k2<3,无解;
2)若k1≥5,f(2T)≥10π,则存在T<x1<x2<2T,使得f(x1)=6π,f(x2)=8π;
则T,x1,x2,2T为cosf(x)=1在[T,2T]上的4个解;
但方程cosf(x)=1在[0,2T]上只有f(x)=0,2π,4π,3个解,矛盾;
3)当k1=4时,f(2T)=8π=f(T)+f(T),结论成立;
③当x∈(0,T)时,f(x)∈(0,4π),考查方程cosf(x)=c在(0,T)上的解;
设其解为f(x1),f(x2),…,f(xn),(x1<x2<…<xn);
则f(x1+T),f(x2+T),…,f(xn+T)为方程cosf(x)=c在(T,2T)上的解;
又f(x+T)∈(4π,8π);
而f(x1)+4π,f(x2)+4π,…,f(xn)+4π∈(4π,8π)为方程cosf(x)=c在(T,2T)上的解;
∴f(xi+T)=f(xi)+4π=f(xi)+f(T);
∴综上对任意x∈[0,T],都有f(x+T)=f(x)+f(T).
点评 考查对余弦周期函数定义的理解,充分条件的概念,方程的解的概念,知道由cosf(x)=1能得出f(x)=2kx,k∈Z,以及构造方程解题的方法,在证明最后一问时能运用第二问的结论.


科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-2,2] | C. | $[{\frac{{\sqrt{3}-3}}{4},\frac{{\sqrt{3}+3}}{4}}]$ | D. | $[{0,\frac{12}{5}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
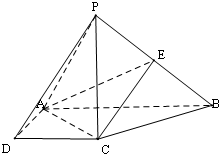 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,PC<2,E是PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,PC<2,E是PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,PA=PB=2,PC=4,∠APB=∠BPC=60°,cos∠APC=$\frac{1}{4}$.
如图,在三棱锥P-ABC中,PA=PB=2,PC=4,∠APB=∠BPC=60°,cos∠APC=$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届河南商丘第一高级中学年高三上理开学摸底数学试卷(解析版) 题型:解答题
已知函数 ,且
,且 .
.
(1)若函数 在区间
在区间 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(2)设函数 ,当
,当 时,
时, 恒成立,求
恒成立,求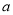 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com