在正六边形ABCDEF中.若$\overrightarrow{AB}$=$\overrightarrow{AC}$+λ$\overrightarrow{AD}$.则λ=-$\frac{1}{2}$．题目和参考答案——青夏教育精英家教网—

8．在正六边形ABCDEF中，若$\overrightarrow{AB}$=$\overrightarrow{AC}$+λ$\overrightarrow{AD}$，则λ=-$\frac{1}{2}$．

分析根据向量加减运算的几何意义求出λ．

解答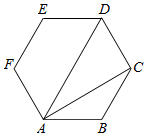解由正六边形的知识可知$\overrightarrow{BC}=\frac{1}{2}$$\overrightarrow{AD}$，
∵$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}$=$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$，
∴$\overrightarrow{AB}$=$\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AD}$．
∴$λ=-\frac{1}{2}$
故答案为：$-\frac{1}{2}$．

点评本题考查了平面向量的线性运算的几何意义，属于基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

20．在△ABC中，A=60°，a=$\sqrt{6}$，b=$\sqrt{3}$，满足条件的△ABC （　　）

A．

无解

B．

仅一解

C．

有两解

D．

不能确定

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

19．设集合M={-1，1}，N={x|x²-x＜6}，则下列结论正确的是（　　）

A．

N⊆M

B．

N∩M=∅

C．

M⊆N

D．

M∩N=R

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

16．已知椭圆Γ：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）过点M（$\sqrt{2}$，0），且离心率为$\frac{\sqrt{2}}{2}$．
（Ⅰ）求椭圆Γ的方程；
（Ⅱ）设点P（x₀，y₀）（y₀≠0）在椭圆Γ上，
（ⅰ）证明：直线$\frac{{x}_{0}x}{2}+{y}_{0}y$=1与椭圆相切；
（ⅱ）过点P作两条直线PA、PB分别交椭圆于点A、B，
求证：“直线AB的斜率与过点P的椭圆的切线斜率互为相反数”的充要条件是“直线PA的斜率与直线PB的斜率互为相反数”．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

3．某工厂生产某种零件，已知日均销售量x（件）与货价P（元）之间的函数关系式为P=160-2x，生产x件成本的函数关系式为C=500+3x．试讨论，该工厂平均日销售量x为何值时，能获得最大利润？并求出最大利润？

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

13．

某校在一次高三年级“诊断性”测试后，对该年级的500名考生的成绩进行统计分析，成绩的频率分布表及频率分布直方图如图所示，规定成绩不小于125分为优秀．
（1）若用分层抽样的方法从这500人中抽取4人的成绩进行分析，求其中成绩为优秀的学生人数；
（2）在（1）中抽取的4名学生中，随机抽取2名学生参加分析座谈会，求恰有1人成绩为优秀的概率．