
分析 (I)利用等差数列的通项公式及其前n项和公式即可得出;
(II)利用“裂项求和”方法即可得出.
解答 解:(Ⅰ)设等差数列{an} 的公差为d,由a5+a7=26,得a6=13,又a6-a3=3d=6,解得d=2.
∴an=a3+(n-3)d=7+2(n-3)=2n+1.
∴以${S_n}=\frac{{{a_1}+{a_n}}}{2}×n=\frac{3+2n+1}{2}×n={n^2}+2n$.
(Ⅱ)由${b_n}=\frac{1}{{{S_n}-n}}$,得${b_n}=\frac{1}{{{n^2}+n}}=\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$.
设{bn} 的前n 项和为Tn,则${T_8}=(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})+…+(\frac{1}{8}-\frac{1}{9})=1-\frac{1}{9}=\frac{8}{9}$.
故数列{bn} 的前8项和为$\frac{8}{9}$.
点评 本题考查了等差数列的通项公式及其前n项和公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | x+y+1=0 | B. | x-y+1=0 | C. | x+2y+1=0 | D. | x+2y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 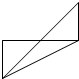 | C. | 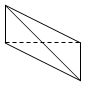 | D. | 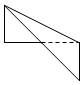 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 编号 | 项目 | 收案(件) | 结案(件) | |
| 判决(件) | ||||
| 1 | 刑事案件 | 2400 | 2400 | 2400 |
| 2 | 婚姻家庭、继承纠纷案件 | 3000 | 2900 | 1200 |
| 3 | 权属、侵权纠纷案件 | 4100 | 4000 | 2000 |
| 4 | 合同纠纷案件 | 14000 | 13000 | n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,6] | B. | [6,+∞) | C. | (-∞,-4] | D. | [-4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com