
分析 (1)求出f′(x)=3x2-4x-4,利用导数性质能求出函数y=f(x)的单调增区间和单调减区间.
(2)由f′(x)=3x2-4x-4=0,得${x}_{1}=-\frac{2}{3}$,x2=2,列表讨论能求出f(x)在[-1,4]上的最大值和最小值.
解答 解:(1)∵函数f(x)=x3-2x2-4x,
∴f′(x)=3x2-4x-4,
由f′(x)>0,得x<-$\frac{2}{3}$或x>2,
由f′(x)<0,得-$\frac{2}{3}$<x<2,
∴函数y=f(x)的单调增区间是(-∞,-$\frac{2}{3}$),[2,+∞);单调减区间是[-$\frac{2}{3}$,2].
(2)由f′(x)=3x2-4x-4=0,
得${x}_{1}=-\frac{2}{3}$,x2=2,
列表,得:
| x | -1 | (-1,-$\frac{2}{3}$) | -$\frac{2}{3}$ | (-$\frac{2}{3}$,2) | 2 | (2,4) | 4 |
| f′(x) | + | 0 | - | 0 | + | ||
| f(x) | 1 | ↑ | $\frac{40}{27}$ | ↓ | -8 | ↑ | 16 |
点评 本题考查导数及其应用、不等式、函数等基础知识,考查考查推理论证能力、运算求解能力、抽象概括能力,考查化归与转化思想、函数与方程思想、分类与整合思想,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
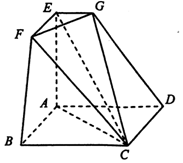 如图所示的空间几何体ABCDEFG中,四边形ABCD是边长为2的正方形,AE⊥平面ABCD,EF∥AB,EG∥AD,EF=EG=1.
如图所示的空间几何体ABCDEFG中,四边形ABCD是边长为2的正方形,AE⊥平面ABCD,EF∥AB,EG∥AD,EF=EG=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,M为AD上的点,AE=1,AM=$\frac{1}{2}$.
边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,M为AD上的点,AE=1,AM=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2和1 | B. | 2和0 | C. | 2和-1 | D. | 2和-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2-2x-4 | B. | x2+x-1 | C. | x2+2x | D. | x2-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x>0,总有(x+1)ex≤1 | B. | ?x≤0,总有(x+1)ex≤1 | ||
| C. | ?x0≤0,总有(x0+1)${e}^{{x}_{0}}$≤1 | D. | ?x0>0,使得(x0+1)${e}^{{x}_{0}}$≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 可能为锐角三角形 | B. | 一定不是锐角三角形 | ||
| C. | 一定为钝角三角形 | D. | 不可能为钝角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com