
分析 (Ⅰ)动点A满足椭圆的定义,由此能求出动点A的轨迹M满足的方程.
(Ⅱ)设P(x0,y0),△PBC的内切圆为⊙O1,半径为r1;△PBC的外接圆为⊙O2,半径为r2,推导出${r_1}=\frac{{|{y_0}|}}{3}$,${O_2}(0,\frac{3}{{2{y_0}}}-\frac{y_0}{6})$,从而$\frac{r_2}{r_1}=\frac{{|{\frac{3}{{2{y_0}}}+\frac{y_0}{6}}|}}{{\frac{{|{y_0}|}}{3}}}=\frac{9}{2y_0^2}+\frac{1}{2}$,由此能求出$\frac{S_2}{S_1}$的最小值.
解答 解:(Ⅰ)根据题意知,动点A满足椭圆的定义(1分)
所以,有|F1F2|=|BC|=2c=2,|AF1|+|AF2|=|AB|+|AC|=2a=4,(2分)
且a2=b2+c2解得$a=2,b=\sqrt{3}$(3分)
所以,动点A的轨迹M满足的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1,(y≠0)$(4分)
没有写出y≠0或x≠±2扣(1分)
(Ⅱ)设P(x0,y0),△PBC的内切圆为⊙O1,半径为r1;△PBC的外接圆为⊙O2,半径为r2,
∵$\frac{1}{2}(4+2){r_1}=\frac{1}{2}×2×|{y_0}|$,∴${r_1}=\frac{{|{y_0}|}}{3}$,(6分)
线段PB的垂直平分线方程为$y-\frac{y_0}{2}=-\frac{{{x_0}+1}}{y_0}(x-\frac{{{x_0}-1}}{2})$(7分)
又线段BC的垂直平分线方程为x=0,
两条垂线方程联立求得$y=(-\frac{{{x_0}+1}}{y_0})(-\frac{{{x_0}-1}}{2})+\frac{y_0}{2}=\frac{x_0^2-1}{{2{y_0}}}+\frac{y_0}{2}$(8分)
∵$\frac{x_0^2}{4}+\frac{y_0^2}{3}=1$,∴$y=\frac{3}{2y}-\frac{y_0}{6}$,
∴⊙O2的圆心为${O_2}(0,\frac{3}{{2{y_0}}}-\frac{y_0}{6})$
∴${r_2}=\sqrt{1+{{(\frac{3}{{2{y_0}}}-\frac{y_0}{6})}^2}}=\sqrt{\frac{9}{4y_0^2}+\frac{y_0^2}{36}+\frac{1}{2}}=|{\frac{3}{{2{y_0}}}+\frac{y_0}{6}}|$(9分)
∴$\frac{r_2}{r_1}=\frac{{|{\frac{3}{{2{y_0}}}+\frac{y_0}{6}}|}}{{\frac{{|{y_0}|}}{3}}}=\frac{9}{2y_0^2}+\frac{1}{2}$,(10分)
∵$y_0^2≤3$,∴$\frac{r_2}{r_1}≥2$,∴$\frac{S_2}{S_1}≥4$
∴${(\frac{S_2}{S_1})_{min}}=4$,此时$y_0^2=3$.(12分)
方法不一样,只要过程正确,答案准确给满分
点评 本题考查点的轨迹方程的求法,考查三角形内切圆与接圆面积之比的最小值的求法,是中档题,解题时要认真审题,注意椭圆、直线、圆等知识点的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
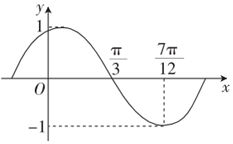 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$),其部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$),其部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{4}$] | B. | [$\frac{1}{4}$,1) | C. | (0,$\frac{1}{2}$] | D. | [$\frac{1}{4}$,$\frac{1}{2}$]∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{12}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com