Question

7．已知函数f（x）=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象在y轴上截距为0，它在y轴右侧的第一个最大值点和最小值点分别为（x₀，$\frac{{-1+\sqrt{2}}}{2}$）；（x₀+π，$\frac{{-1-\sqrt{2}}}{2}$）．
（Ⅰ）求f（x）的解析式；
（Ⅱ）若函数g（x）=f（x）+m|x+$\frac{3π}{4}}$|（m＞0）在[-$\frac{11π}{12}$，-$\frac{π}{2}$]上存在零点，求实数m的取值范围．

Answer 1

分析 （Ⅰ）由函数的图象的顶点坐标求出A、B，由周期求出ω，由特殊点的坐标求出φ的值，可得函数的解析式．
（Ⅱ）由题意可得函数y=$\frac{1}{2}$-$\frac{\sqrt{2}}{2}$sinx的图象和函数y=m|x+$\frac{3π}{4}$|的图象有交点，数形结合求得m的范围．

解答 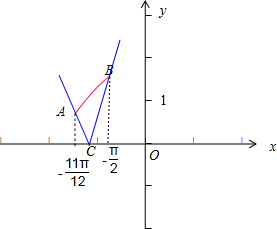解：（Ⅰ）由函数f（x）=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象在y轴上截距为0，
可得函数的图象经过点（0，0），
故Asinφ=0，∴φ=0．
根据它在y轴右侧的第一个最大值点和最小值点
分别为（x₀，$\frac{{-1+\sqrt{2}}}{2}$）；（x₀+π，$\frac{{-1-\sqrt{2}}}{2}$），
可得$\frac{1}{2}$•$\frac{2π}{ω}$=π，且B=$\frac{\frac{-1+\sqrt{2}}{2}+\frac{-1-\sqrt{2}}{2}}{2}$=-$\frac{1}{2}$，
∴A=$\frac{-1+\sqrt{2}}{2}$-（-$\frac{1}{2}$）=$\frac{\sqrt{2}}{2}$，∴ω=1，
∴函数f（x）=$\frac{\sqrt{2}}{2}$sinx-$\frac{1}{2}$．
（Ⅱ）∵函数g（x）=f（x）+m|x+$\frac{3π}{4}}$|=$\frac{\sqrt{2}}{2}$sinx-$\frac{1}{2}$+m|x+$\frac{3π}{4}$|（m＞0）在[-$\frac{11π}{12}$，-$\frac{π}{2}$]上存在零点，
∴函数y=$\frac{1}{2}$-$\frac{\sqrt{2}}{2}$sinx的图象和函数y=m|x+$\frac{3π}{4}$|的图象有交点．
∵sin（-$\frac{11π}{12}$）=-sin$\frac{11π}{12}$=-sin$\frac{π}{12}$=-$\sqrt{\frac{1-cos\frac{π}{6}}{2}}$=-$\frac{\sqrt{2-\sqrt{3}}}{2}$，
在[-$\frac{11π}{12}$，-$\frac{π}{2}$]上，sinx∈[-1，-$\frac{\sqrt{2-\sqrt{3}}}{2}$]，故 y=$\frac{1}{2}$-$\frac{\sqrt{2}}{2}$sinx∈[$\frac{\sqrt{3}+1}{4}$，$\frac{1+\sqrt{2}}{2}$]．
设A（-$\frac{11π}{12}$，$\frac{\sqrt{3}+1}{4}$）、B（-$\frac{π}{2}$，$\frac{1+\sqrt{2}}{2}$）、C（-$\frac{3π}{4}$，0），
则y=$\frac{1}{2}$-$\frac{\sqrt{2}}{2}$sinx的图象（图中红色部分）经过点A、B，由于函数y=m|x+$\frac{3π}{4}$|的图象经过点C．
由于直线CA的斜率为-$\frac{3+3\sqrt{3}}{2π}$，CB的斜率为2+2$\sqrt{2}$，
故m应大于0，且m大于或等于CA、CB的斜率中绝对值较小的，
∴实数m的取值范围为{m|m≥$\frac{3+3\sqrt{3}}{2π}$}．

点评 本题主要考查正弦函数的图象的特征，由函数y=Asin（ωx+φ）的部分图象求解析式，由函数的图象的顶点坐标求出A、B，由周期求出ω，由特殊点的坐标求出φ的值，属于中档题．