
分析 先确定曲线的性质,然后结合图形确定临界状态,结合直线与圆相交的性质,可解得k的取值范围.
解答  解:y=1+$\sqrt{4-{x^2}}$可化为x2+(y-1)2=4,y≥1,所以曲线为以(0,1)为圆心,2为半径的圆y≥1的部分.
解:y=1+$\sqrt{4-{x^2}}$可化为x2+(y-1)2=4,y≥1,所以曲线为以(0,1)为圆心,2为半径的圆y≥1的部分.
直线y=k(x-2)+4过定点P(2,4),由图知,当直线经过A(-2,1)点时恰与曲线有两个交点,顺时针旋转到与曲线相切时交点变为一个.
且kAP=$\frac{3}{4}$,由直线与圆相切得d=$\frac{|-1+4-2k|}{\sqrt{{k}^{2}+1}}$=2,解得k=$\frac{5}{12}$.
则实数k的取值范围为$\frac{5}{12}<k≤\frac{3}{4}$.
故答案为:$\frac{5}{12}<k≤\frac{3}{4}$.
点评 本题考查直线与圆相交的性质,同时考查了学生数形结合的能力,是个基础题.


科目:高中数学 来源: 题型:解答题
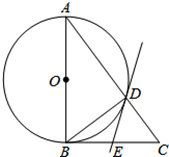 如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(3,+∞) | B. | (-∞,-1)∪[3,+∞) | C. | (-2,1] | D. | (-2,-1]∪[3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 44 | B. | 54 | C. | 88 | D. | 108 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com