
分析 ①由于a1=0,且对任意的n∈N*,均有|an+1-an|=n,则n=1时,|a2-0|=1,解得a2=±1.利用|a3-a2|=2,即可得出a3.
②对任意的n∈N*,均有|an+1-an|=n,可得:an+1-an=±n,取an+1-an=n,a1=0时,数列{an}单调递增,利用“累加求和”方法即可得出.
解答 解:①∵a1=0,且对任意的n∈N*,均有|an+1-an|=n,
∴n=1时,|a2-0|=1,解得a2=±1.
∴a2=1,则|a3-1|=2,解得a3=3,-1.
∴a2=-1,则|a3+1|=2,解得a3=-3,1.
∴a3所有可能的取值构成的集合为{-3,-1,1,3}.
②对任意的n∈N*,均有|an+1-an|=n,可得:an+1-an=±n,
取an+1-an=n,a1=0时,数列{an}单调递增,
可得:an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=(n-1)+(n-2)+…+1+0
=$\frac{n(n-1)}{2}$,
则a64的最大值=$\frac{64×63}{2}$=2016.
故答案为:{-3,-1,1,3},2016.
点评 本题考查了数列递推关系、等差数列的通项公式、数列的单调性,考查了分类讨论方法、推理能力与计算能力,属于难题.


 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:解答题
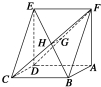 如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{16}$ | B. | 1 | C. | $\frac{25}{48}$ | D. | $\frac{25}{64}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
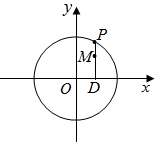 如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=$\frac{4}{5}$|PD|.
如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=$\frac{4}{5}$|PD|.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于直线y=x对称 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com