
【题目】在平面直角坐标系![]() 中,已知半径为
中,已知半径为![]() 的圆
的圆![]() ,圆心在
,圆心在![]() 轴正半轴上,且与直线
轴正半轴上,且与直线![]() 相切.
相切.
(1)求圆![]() 的方程;
的方程;
(2)在圆![]() 上,是否存在点
上,是否存在点![]() ,满足
,满足![]() ,其中,点
,其中,点![]() 的坐标是
的坐标是![]() .若存在,指出有几个这样的点;若不存在,请说明理由;
.若存在,指出有几个这样的点;若不存在,请说明理由;
(3)若在圆![]() 上存在点
上存在点![]() ,使得直线
,使得直线![]() 与圆
与圆![]() 相交不同两点
相交不同两点![]() ,求
,求![]() 的取值范围.并求出使得
的取值范围.并求出使得![]() 的面积最大的点
的面积最大的点![]() 的坐标及对应的
的坐标及对应的![]() 的面积.
的面积.
【答案】(1)![]() ;(2)不存在点
;(2)不存在点![]() 满足条件;(3)
满足条件;(3)![]() ,
,![]() .
.
【解析】
试题分析:(1)设圆心坐标是![]() ,可根据点到直线距离公式求得
,可根据点到直线距离公式求得![]() ,即可得到圆
,即可得到圆![]() 的方程;(2)假设存在这样的点
的方程;(2)假设存在这样的点![]() ,则有
,则有![]() ,然后判断
,然后判断![]() 与
与![]() 有无交点即可;(3)根据圆心到直线的距离小于半径即可求
有无交点即可;(3)根据圆心到直线的距离小于半径即可求![]() 的取值范围,
的取值范围,![]() 的面积表示为关于
的面积表示为关于![]() 的函数,利用配方法可求最值.
的函数,利用配方法可求最值.
试题解析:(1)设圆心是![]() ,它到直线
,它到直线![]() 的距离是
的距离是![]() ,解得
,解得![]() 或
或![]() (舍去),所以,所求圆
(舍去),所以,所求圆![]() 的方程是
的方程是![]() .
.
(2)假设存在这样的点![]() ,则由
,则由![]() ,得
,得![]() .
.
即,点P在圆D:![]() 上,点P也在圆C:
上,点P也在圆C:![]() 上.
上.
因为![]() ,所以圆C与圆D外离,圆C与圆D没有公共点.所以,不存在点
,所以圆C与圆D外离,圆C与圆D没有公共点.所以,不存在点![]() 满足条件.
满足条件.
(3)存在,理由如下:因为点![]() 在圆
在圆![]() 上,所以
上,所以![]() ,
,![]() 且
且![]() .
.
因为原点到直线![]() 的距离
的距离![]() ,解得
,解得![]()
而![]() ,所以
,所以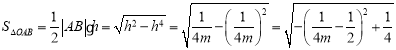 ,
,
因为![]() ,所以当
,所以当![]() ,即
,即![]() 时,
时,![]() 取得最大值
取得最大值![]() ,
,
此时点![]() 的坐标是
的坐标是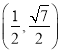 或
或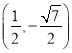 ,
,![]() 的面积的最大值是
的面积的最大值是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在P地正西方向8km的A处和正东方向1km的B处各有一条正北方向的公路AC和BD,现计划在AC和BD路边各修建一个物流中心E和F,为缓解交通压力,决定修建两条互相垂直的公路PE和PF,设![]()

![]() Ⅰ
Ⅰ![]() 为减少对周边区域的影响,试确定E,F的位置,使
为减少对周边区域的影响,试确定E,F的位置,使![]() 与
与![]() 的面积之和最小;
的面积之和最小;
![]() Ⅱ
Ⅱ![]() 为节省建设成本,求使
为节省建设成本,求使![]() 的值最小时AE和BF的值.
的值最小时AE和BF的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查一款电视机的使用时间,研究人员对该款电视机进行了相应的测试,将得到的数据统计如下图所示:
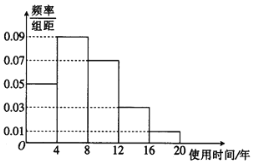
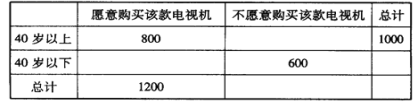
并对不同年龄层的市民对这款电视机的购买意愿作出调查,得到的数据如下表所示:
(1)根据图中的数据,试估计该款电视机的平均使用时间;
(2)根据表中数据,判断是否有99.9%的把握认为“愿意购买该款电视机”与“市民的年龄”有关;
(3)若按照电视机的使用时间进行分层抽样,从使用时间在[0,4)和[4,20]的电视机中抽取5台,再从这5台中随机抽取2台进行配件检测,求被抽取的2台电视机的使用时间都在[4,20]内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在R上的奇函数,且满足
是定义在R上的奇函数,且满足![]() ,
,![]() =1,数列{
=1,数列{![]() }满足
}满足![]() =﹣1,
=﹣1, ![]() (
(![]() ),其中
),其中![]() 是数列{
是数列{![]() }的前n项和,则
}的前n项和,则![]() =
=
A. ﹣2 B. ﹣1 C. 0 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了选拔参加自行车比赛的选手,对自行车运动员甲、乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息;
(2)估计甲、乙两运动员的最大速度的平均数和方差,并判断谁参加比赛更合适.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 同时满足:①对于定义域上的任意
同时满足:①对于定义域上的任意![]() ,恒有
,恒有![]() ;②对于定义域上的任意
;②对于定义域上的任意![]() ,当
,当![]() 时,恒有
时,恒有![]() ,则称函数
,则称函数![]() 为“理想函数”.给出下列四个函数中:①
为“理想函数”.给出下列四个函数中:① ![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④ 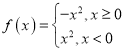 ,能被称为“理想函数”的有_____(请将所有正确命题的序号都填上).
,能被称为“理想函数”的有_____(请将所有正确命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足条件
满足条件![]() 是偶函数,
是偶函数, ![]() ,且
,且![]() 的图象与直线
的图象与直线![]() 恰有一个公共点.
恰有一个公共点.
(1)求![]() 的解析式;
的解析式;
(2)设![]() ,是否存在实数
,是否存在实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上的最大值为2?如果存在,求出
上的最大值为2?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成![]() 两组,每组100只,其中
两组,每组100只,其中![]() 组小鼠给服甲离子溶液,
组小鼠给服甲离子溶液,![]() 组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:

记![]() 为事件:“乙离子残留在体内的百分比不低于
为事件:“乙离子残留在体内的百分比不低于![]() ”,根据直方图得到
”,根据直方图得到![]() 的估计值为
的估计值为![]() .
.
(1)求乙离子残留百分比直方图中![]() 的值;
的值;
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com