Question

4．已知函数f（x）=xe^x-ae^x-1，且f′（1）=e．
（1）求a的值及f（x）的单调区间；
（2）若关于x的方程f（x）=kx²-2（k＞2）存在两个不相等的正实数根x₁，x₂，证明：|x₁-x₂|＞ln（$\frac{4}{e}$）．

Answer 1

分析 （1）f′（x）=e^x+xe^x-ae^x-1，由f′（1）=e．解得a=e．可得f′（x）=xe^x．分别解出f′（x）＞0，f′（x）＜0，函即可得出函数f（x）的单调区间．
（2）方程f（x）=kx²-2（k＞2），即（x-1）e^x-（kx²-2）=0，令g（x）=（x-1）e^x-（kx²-2），令g′（x）=0，解得x=0或ln（2k）．k＞2，可得ln（2k）＞1．不妨设x₁＜x₂．可得：0＜x₁＜1＜ln（2k）＜x₂．即可证明．

解答 （1）解：f′（x）=e^x+xe^x-ae^x-1，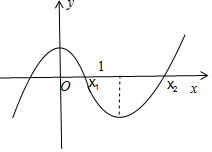
∴f′（1）=e+e-a=e．解得a=e．
∴f′（x）=e^x+xe^x-ee^x-1=xe^x．
∴x＞0时，f′（x）＞0，函数f（x）单调递增；x＜0时，
f′（x）＜0，函数f（x）单调递减．
即函数f（x）单调递增区间为（0，+∞）；函数f（x）单调递减区间为（-∞，0]．
（2）证明：方程f（x）=kx²-2（k＞2），
即（x-1）e^x-（kx²-2）=0，
令g（x）=（x-1）e^x-（kx²-2），
g′（x）=xe^x-2kx=x（e^x-2k），
令g′（x）=0，解得x=0或ln（2k）．
∵k＞2，∴ln（2k）＞1．
g（0）=1，g（1）=2-k＜0，g（ln（2k））＜0．x→+∞时，g（x）→+∞．
因此关于x的方程f（x）=kx²-2（k＞2）存在两个不相等的正实数根x₁，x₂，不妨设x₁＜x₂．
可得：0＜x₁＜1＜ln（2k）＜x₂．
∴|x₁-x₂|＞ln（2k）-1=$ln\frac{2k}{e}$＞ln（$\frac{4}{e}$）．

点评 本题考查了利用导数研究函数的单调性极值与最值、方程与不等式的解法、数形结合方法，考查了推理能力与计算能力，属于难题．