练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．已知$\frac{sinx+1}{cosx}=\frac{1}{2}$，则$\frac{sinx-1}{cosx}$的值是（　　）
    A．$\frac{1}{2}$B．2C．$-\frac{1}{2}$D．-2

    分析 根据同角三角函数关系式即可求解．

    解答 解：由$\frac{sinx+1}{cosx}=\frac{1}{2}$，可得：sinx=$\frac{1}{2}cosx$-1，（cosx≠0）
    sin2x+cos2x=1，
    ∴（$\frac{1}{2}cosx$-1）2+cos2x=1，
    得：$\frac{5}{4}$cos2x-cosx=0，
    解得：cosx=$\frac{4}{5}$．
    那么：$\frac{sinx-1}{cosx}=\frac{sin+1-2}{cosx}=\frac{1}{2}-\frac{2}{cosx}$=-2．
    故选D

    点评 本题主要考察了同角三角函数关系式的应用，属于基本知识的考查．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

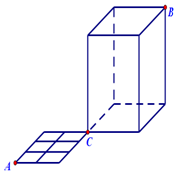    9．如图，一只蚂蚁从点A出发沿着水平面的线条爬行到点C，再由点C沿着置于水平面的长方体的棱爬行至顶点B，则它可以爬行的不同的最短路径有（　　）条．
    A．40B．60C．80D．120

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．下列图形中，不可能是函数y=f（x）的图象的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．用数学归纳法证明：（n+1）（n+2）…（n+n）=2n×1×3×…×（2n-1）时，从“k到k+1”左边需增加的代数式是（k+1）（k+2）…（k+k）（4k+1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．cos555°的值为（　　）
    A．$\frac{{\sqrt{6}+\sqrt{2}}}{4}$B．$\frac{{\sqrt{6}-\sqrt{2}}}{4}$C．$-\frac{{\sqrt{6}+\sqrt{2}}}{4}$D．$\frac{{\sqrt{2}-\sqrt{6}}}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知F1，F2是椭圆和双曲线的公共焦点，P是它们的一个公共点，且$∠{F_1}P{F_2}=\frac{π}{3}$，则椭圆和双曲线的离心率乘积的最小值为（　　）
    A．1B．$\frac{{\sqrt{3}}}{2}$C．$\sqrt{2}$D．$\frac{{\sqrt{6}}}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．执行如图所示的程序框图，则输出的S的值为（　　）
    A．4B．5C．6D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．用辗转相除法求1813和333的最大公约数时，需要做3次除法．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知g（x）=sin2x，将g（x）的图象向左平移$\frac{π}{8}$个单位长度，再将图象上各点的横坐标缩短到原来的$\frac{1}{4}$，得到函数f（x）的图象，则（　　）
    A．$f（x）=sin（8x-\frac{π}{4}）$B．$f（x）=sin（8x+\frac{π}{4}）$C．$f（x）=sin（\frac{x}{2}-\frac{π}{4}）$D．$f（x）=sin（\frac{x}{2}+\frac{π}{4}）$

    查看答案和解析>>

    同步练习册答案