
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
分析 利用条件得出△ABP是等腰三角形,且AB=BP,可得a,c的关系,即可求出双曲线的离心率.
解答 解:设AP的中点为C,则
∵$\overrightarrow{BA}$•$\overrightarrow{AP}$+$\overrightarrow{BP}$•$\overrightarrow{AP}$=($\overrightarrow{BA}$+$\overrightarrow{BP}$)•$\overrightarrow{AP}$=0,
∴$\overrightarrow{BC}$⊥$\overrightarrow{AP}$,
∴△ABP是等腰三角形,且AB=BP,
∴2a=$\sqrt{(c-a)^{2}+{b}^{2}}$,
∴2a2=c2-ac,
∴e2-e-2=0,
∵e>1,
∴e=2.
故选:C.
点评 本题考查双曲线的离心率,考查向量知识的运用,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
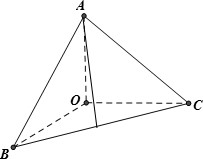 如图所示,在三棱锥A-OBC中,OA,OB,OC两两垂直且长度都为2,则这个三棱锥的体积为$\frac{4}{3}$;O到平面ABC的距离为$\frac{2\sqrt{3}}{3}$.
如图所示,在三棱锥A-OBC中,OA,OB,OC两两垂直且长度都为2,则这个三棱锥的体积为$\frac{4}{3}$;O到平面ABC的距离为$\frac{2\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n∥α,则m∥n | B. | 若m⊥α,n⊥α,则m∥n | ||
| C. | 若m∥α,n∥α,β∥α,则m∥n | D. | 若m∥n,m∥α,则n∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 5吨 | 0.9万元 | 0.3万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{225}$ | B. | $\frac{1}{300}$ | C. | $\frac{1}{450}$ | D. | 以上全不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向右平移$\frac{π}{8}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向左平移$\frac{π}{8}$个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com