
 如图,P是正方体ABCD-A1B1C1D1表面对角线A1C1上的一个动点,正方体的棱长为1,
如图,P是正方体ABCD-A1B1C1D1表面对角线A1C1上的一个动点,正方体的棱长为1,分析 (1)如图所示,连接DC,AC,DC∩AC=O,由正方形的性质可得:AC⊥BD,利用线面垂直的性质定理可得:AA1⊥BD.即可证明BD⊥平面ACC1A1,进而得出PA与DB所成角.
(2)由DC∥AB,可得DC∥平面PAB,因此直线DC上的任意一点到平面的距离即为DC到面PAB距离d.当点P取点C1时,d取得最小值;当点P取点A1时,d取得最大值,即可得出DC到面PAB距离d的取值范围.
(3)过点P分别作PM⊥AB,PN⊥BC,M,N分别为垂足,作PE⊥平面ABCD,垂足为E,连接EM,EN.由三垂线定理可得:AB⊥EM,BC⊥EN,EM+EN=1.则∠PME是二面角P-AB-D的平面角,∠PNE是二面角P-BC-D的平面角,可得tanα=$\frac{1}{EM}$,tanβ=$\frac{1}{EN}$.tan(α+β)=$\frac{1}{EM•EN-1}$,由1=EM+EN≥2$\sqrt{EN•EB}$,即可得出.
解答 解:(1)如图所示,连接DC,AC,DC∩AC=O,∵四边形ABCD是正方形,∴AC⊥BD,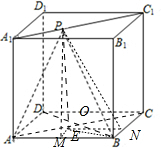
又AA1⊥底面ABCD,BD?平面ABCD,∴又AA1⊥BD.
又AA1∩AC=A,∴BD⊥平面ACC1A1,PA?平面ACC1A1,
∴BD⊥PA.∴PA与DB所成角为90°.
(2)∵DC∥AB,DC?平面PAB,AB?平面PAB,
∴DC∥平面PAB,因此直线DC上的任意一点到平面的距离即为DC到面PAB距离d.
当点P取点C1时,d取得最小值,点C到对角面ABC1的距离d=$\frac{1}{2}{B}_{1}C$=$\frac{\sqrt{2}}{2}$.
当点P取点A1时,d取得最大值,点C到侧面ABB1A1的距离d=BC=1.
∴DC到面PAB距离d的取值范围是$[\frac{\sqrt{2}}{2},1]$.
(3)过点P分别作PM⊥AB,PN⊥BC,M,N分别为垂足,作PE⊥平面ABCD,垂足为E,连接EM,EN.
由三垂线定理可得:AB⊥EM,BC⊥EN,EM+EN=1.
则∠PME是二面角P-AB-D的平面角,∠PNE是二面角P-BC-D的平面角,
∴∠PME=α,∠PNE=β.
则tanα=$\frac{1}{EM}$,tanβ=$\frac{1}{EN}$.
tan(α+β)=$\frac{\frac{1}{EM}+\frac{1}{EN}}{1-\frac{1}{EM}•\frac{1}{EN}}$=$\frac{EM+EN}{EM•EN-1}$=$\frac{1}{EM•EN-1}$,
∵1=EM+EN≥2$\sqrt{EN•EB}$,当且仅当EN=EM=$\frac{1}{2}$时取等号,
∴tan(α+β)的最小值为$\frac{1}{\frac{1}{4}-1}$=-$\frac{4}{3}$.
∴α+β最小时的正切值为$-\frac{4}{3}$.
点评 本题考查了空间位置关系与空间角、线面平行与垂直的判定与性质定理、正方形的性质、直角三角形的边角关系、基本不等式的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{4}$ | B. | 0或$-\frac{1}{4}$ | C. | 0或-1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持 | 反对 | 合计 | |
| 男性 | 20 | 10 | 30 |
| 女性 | 40 | 30 | 70 |
| 合计 | 60 | 40 | 100 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 该四面体的三组对棱的中点连线两两垂直 | |
| B. | 该四面体的外接球球心与内切球球心重合 | |
| C. | 该四面体的各面是全等的锐角三角形 | |
| D. | 该四面体中任意三个面两两所成二面角的正弦值之和为1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.146 2 | B. | 0.153 8 | C. | 0.996 2 | D. | 0.853 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com