
分析 利用垂直平分线转换线段的关系得到|MA|+|MB|=|MA|+|MP|=|AP|=6,据椭圆的定义即可得到动点M的轨迹方程.
解答 解:∵线段PB的垂直平分线l交线段PA于点M,
∴|MA|+|MB|=|MA|+|MP|=|AP|=6,
即M点的轨迹为以A、B为焦点的椭圆,2a=6,c=2,
∴b=$\sqrt{5}$
∴M点的方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}$=1.
故答案为:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}$=1.
点评 定义法:运用解析几何中一些常用定义(例如圆锥曲线的定义),可从曲线定义出发直接写出轨迹方程,或从曲线定义出发建立关系式,从而求出轨迹方程.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{10}{3}$ | B. | -$\frac{10}{3}$ | C. | -$\frac{20}{3}$ | D. | $\frac{20}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,则ac2>bc2 | B. | 若a>b,则a2>b2 | ||
| C. | 若a<b<0,则a2<ab<b2 | D. | 若a<b<0,则$\frac{a}{b}$>$\frac{b}{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDE中,正方形ADEF与梯形ABCD所在平面互相垂直,AB∥CD,AD⊥CD,AB=AD=1,CD=2,M、N分别为EC、BD的中点.
如图,在多面体ABCDE中,正方形ADEF与梯形ABCD所在平面互相垂直,AB∥CD,AD⊥CD,AB=AD=1,CD=2,M、N分别为EC、BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
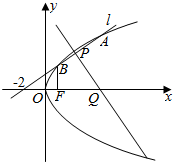 如图,设抛物线y2=4x的焦点为F,过点(-2,0)的直线l交抛物线于A,B两点,线段AB的中垂线分别与AB,x轴交于P,Q两点.若P,Q,F,B四点共圆,则该圆的半径是$\frac{\sqrt{65}}{4}$.
如图,设抛物线y2=4x的焦点为F,过点(-2,0)的直线l交抛物线于A,B两点,线段AB的中垂线分别与AB,x轴交于P,Q两点.若P,Q,F,B四点共圆,则该圆的半径是$\frac{\sqrt{65}}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com