
已知函数 .
.
(1)若直线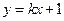 与
与 的反函数的图象相切,求实数k的值;
的反函数的图象相切,求实数k的值;
(2)设 ,讨论曲线
,讨论曲线 与曲线
与曲线 公共点的个数;
公共点的个数;
(3)设 ,比较
,比较 与
与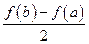 的大小,并说明理由.
的大小,并说明理由.
(1) 
(2)见解析;
(3) 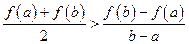
【解析】(1) 的反函数为
的反函数为 .
.
设直线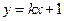 与
与 的图象在
的图象在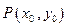 处相切,则
处相切,则
 ,解得
,解得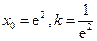 .
.
(2)曲线 与
与 的公共点个数等于曲线
的公共点个数等于曲线 与y=m的公共点个数.
与y=m的公共点个数.
令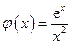 ,则
,则 ,∴
,∴ .
.
当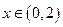 时,
时, ,
,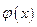 在(0,2)上单调递减;
在(0,2)上单调递减;
当 时,
时, ,
,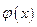 在(2,+∞)上单调递增,
在(2,+∞)上单调递增,
∴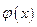 在(0,+∞)上的最小值为
在(0,+∞)上的最小值为 .
.
当 时,曲线
时,曲线 与y=m无公共点;
与y=m无公共点;
当 ,曲线
,曲线 与y=m恰有一个公共点;
与y=m恰有一个公共点;
当 时,在区间(0,2)内存在
时,在区间(0,2)内存在 ,使得
,使得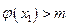 ,在(2,+∞)内存在
,在(2,+∞)内存在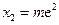 ,使得
,使得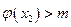 .
.
由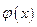 的单调性知,曲线
的单调性知,曲线 与y=m在(0,+∞)上恰有两个公共点.
与y=m在(0,+∞)上恰有两个公共点.
综上所述,当x>0时,
若 ,曲线
,曲线 与
与 没有公共点;
没有公共点;
若 ,曲线
,曲线 与
与 有一个公共点;
有一个公共点;
若 ,曲线
,曲线 与
与 有两个公共点.
有两个公共点.

(3)解法一:可以证明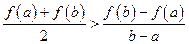 .事实上,
.事实上,

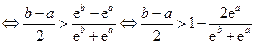
 .(*)
.(*)
令 ,
,
则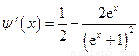 ,
,
 (当且仅当x=0时等号成立),
(当且仅当x=0时等号成立),
∴ 在[0,+∞)上单调递增,
在[0,+∞)上单调递增,
∴ 时,
时,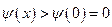 .
.
令 ,即得(*)式,结论得证.
,即得(*)式,结论得证.
解法二:
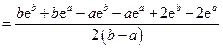
 ,
,
设函数 ,
,
则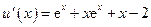 ,
,
令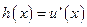 ,则
,则 (当且仅当x=0时等号成立),
(当且仅当x=0时等号成立),
∴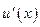 单调递增,
单调递增,
∴当x>0时,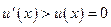 ,∴
,∴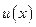 单调递增.
单调递增.
当x>0时,u(x)>u(0)=0.
令 ,得
,得 ,
,
∴ ,
,
因此,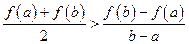 .
.


 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源:2014高考名师推荐数学理科坐标系(解析版) 题型:填空题
已知曲线C的参数方程为 (t为参数),C在点(1,1)处的切线为l.以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,则l的极坐标方程为 .
(t为参数),C在点(1,1)处的切线为l.以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,则l的极坐标方程为 .
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科利用导数求最值和极值(解析版) 题型:选择题
已知函数 .若直线l过点(0,-1),并且与曲线y=f(x)相切,则直线l的方程为( )
.若直线l过点(0,-1),并且与曲线y=f(x)相切,则直线l的方程为( )
A.x+y-1=0
B.x-y-1=0
C.x+y+1=0
D.x-y+1=0
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科几何证明选讲(解析版) 题型:解答题
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.
(1)证明:DB=DC;
(2)设圆的半径为1,BC= ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.

查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科全称量词与存在性量词(解析版) 题型:选择题
已知命题p:?x1,x2∈R,(f(x2)-f(x1))(x2-x1)≥0,则?p是( )
A.?x1,x2∈R,(f(x2)-f(x1))(x2-x1)≤0
B.?x1,x2∈R,(f(x2)-f(x1))(x2-x1)≤0
C.?x1,x2∈R,(f(x2)-f(x1))(x2-x1)<0
D.?x1,x2∈R,(f(x2)-f(x1))(x2-x1)<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com