
| A. | a=1,b=3 | B. | a=3,b=1 | C. | a=$\frac{23}{56}$,b=$\frac{9}{14}$ | D. | a=$\frac{11}{8}$,b=$\frac{3}{2}$ |
分析 求出函数f(x)的导数,可得切线的斜率和切点,由已知切线的方程可得a,b的方程组,解方程即可得到a,b的值.
解答 解:函数f(x)=ax-$\frac{b}{x}$的导数为f′(x)=a+$\frac{b}{{x}^{2}}$,
可得y=f(x)在点(2,f(2))处的切线斜率为a+$\frac{b}{4}$,
切点为(2,2a-$\frac{b}{2}$),
由切线方程7x-4y-12=0,可得a+$\frac{b}{4}$=$\frac{7}{4}$,2a-$\frac{b}{2}$=$\frac{1}{2}$,
解得a=1,b=3.
故选:A.
点评 本题考查导数的运用:求切线的斜率,考查导数的几何意义,正确求导和运用直线方程是解题的关键,属于基础题.


科目:高中数学 来源: 题型:解答题
| 上春晚次数x(单位:次) | 2 | 4 | 6 | 8 | 10 |
| 粉丝数量y(单位:万人) | 15 | 25 | 50 | 70 | 90 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
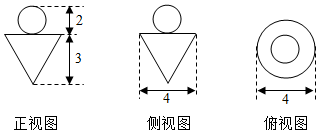 甲几何体(上)与乙几何体(下)的组合体的三视图如图所示,甲、乙的体积分别为V1、V2,则V1:V2等于( )
甲几何体(上)与乙几何体(下)的组合体的三视图如图所示,甲、乙的体积分别为V1、V2,则V1:V2等于( )| A. | 1:4 | B. | 1:3 | C. | 2:3 | D. | 1:π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 4 | 5 |
| y | 1 | 3 | 5 | 7 |
| A. | -0.1 | B. | -0.2 | C. | 0.1 | D. | 0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 152种 | B. | 54种 | C. | 90种 | D. | 126种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com