
已知函数 ,其中a,b∈R
,其中a,b∈R
(1)求函数f(x)的最小值;
(2)当a>0,且a为常数时,若函数h(x)=x[g(x)+1]对任意的x1>x2≥4,总有 成立,试用a表示出b的取值范围;
成立,试用a表示出b的取值范围;
(3)当 时,若
时,若 对x∈[0,+∞)恒成立,求a的最小值.
对x∈[0,+∞)恒成立,求a的最小值.
(1)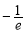 ;(2)
;(2)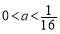 时,
时,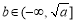 ,
,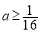 时,
时,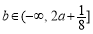 ;(3)1
;(3)1
【解析】
试题分析:(1)利用导数判断出函数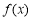 的单调性,即可求出
的单调性,即可求出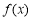 的最小值;(2)解决本题的关键是由“对任意的x1>x2≥4,总有
的最小值;(2)解决本题的关键是由“对任意的x1>x2≥4,总有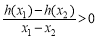 成立”得出“
成立”得出“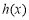 在
在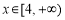 上单调递增”,从而再次转化为导函数大于0的问题求解;(3)通过构造函数
上单调递增”,从而再次转化为导函数大于0的问题求解;(3)通过构造函数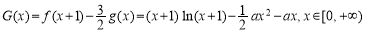 ,转化为
,转化为 对
对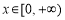 恒成立,于是转化为求
恒成立,于是转化为求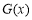 在
在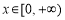 上的最大值问题求解.解题过程中要注意对参数的合理分类讨论.
上的最大值问题求解.解题过程中要注意对参数的合理分类讨论.
试题解析:(1)∵ ,令
,令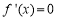 ,得
,得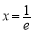
∴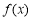 在(0,
在(0,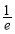 )上单调递减,在(
)上单调递减,在(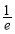 ,+∞)上单调递增
,+∞)上单调递增
∴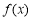 在
在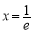 处取得最小值
处取得最小值
即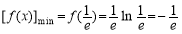 ; 4分
; 4分
(2)由题意,得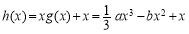 在
在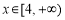 上单调递增
上单调递增
∴ 在
在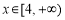 上恒成立
上恒成立
∴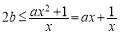 在
在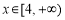 上恒成立 5分
上恒成立 5分
构造函数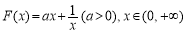
则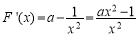
∴F(x)在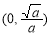 上单调递减,在
上单调递减,在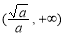 上单调递增
上单调递增
(i)当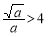 ,即
,即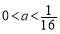 时,F(x)在
时,F(x)在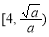 上单调递减,在
上单调递减,在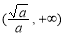 上单调递增
上单调递增
∴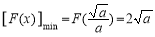
∴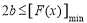 ,从而
,从而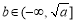 7分
7分
(ii)当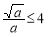 ,即
,即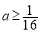 时,F(x)在(4,+∞)上单调递增
时,F(x)在(4,+∞)上单调递增
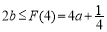 ,从而
,从而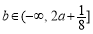 8分
8分
综上,当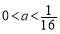 时,
时,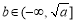 ,
,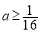 时,
时,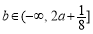 ; 9分
; 9分
(3)当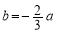 时,构造函数
时,构造函数
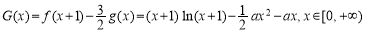
由题意,有 对
对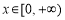 恒成立
恒成立
∵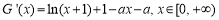
(i)当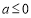 时,
时,
∴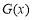 在
在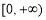 上单调递增
上单调递增
∴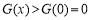 在
在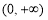 上成立,与题意矛盾. 11分
上成立,与题意矛盾. 11分
(ii)当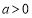 时,令
时,令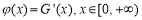
则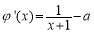 ,由于
,由于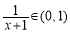
①当 时,
时, ,
,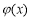 在
在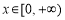 上单调递减
上单调递减
∴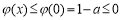 ,即
,即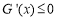 在
在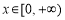 上成立
上成立
∴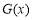 在
在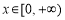 上单调递减
上单调递减
∴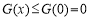 在
在 上成立,符合题意 12分
上成立,符合题意 12分
②当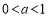 时,
时,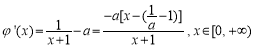
∴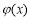 在
在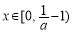 上单调递增,在
上单调递增,在 上单调递减
上单调递减
∵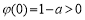
∴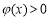 在
在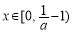 成立,即
成立,即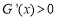 在
在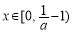 成立
成立
∴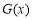 在
在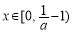 上单调递增
上单调递增
∴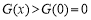 在
在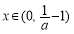 上成立,与题意矛盾 13分
上成立,与题意矛盾 13分
综上,a的最小值为1 14分
考点:导数,函数的单调性,范围与最值,分类与整合.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届四川省成都市高新区高三9月月考理科数学试卷(解析版) 题型:选择题
已知 ,若
,若 是
是 的最小值,则
的最小值,则 的取值范围为( )
的取值范围为( )
(A)[-1,2] (B)[-1,0] (C)[1,2] (D)
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高新区高三9月月考文科数学试卷(解析版) 题型:选择题
将函数 的图象向左平移
的图象向左平移 个单位长度,所得图象对应的函数( )
个单位长度,所得图象对应的函数( )
(A)在区间 上单调递减 (B)在区间
上单调递减 (B)在区间 上单调递增
上单调递增
(C)在区间 上单调递减 (D)在区间
上单调递减 (D)在区间 上单调递增
上单调递增
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市毕业班摸底测试理科数学试卷(解析版) 题型:解答题
已知等差数列 的前n项和为
的前n项和为 ,且
,且
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前n项和Tn.
的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市毕业班摸底测试理科数学试卷(解析版) 题型:选择题
已知定义在R上的偶函数f(x)满足f(4-x)=f(x),且当x∈(-1,3]时,f(x)= ,则函数g(x)=f(x)-|lgx|的零点个数是( )
,则函数g(x)=f(x)-|lgx|的零点个数是( )
A、7 B、8 C、9 D、10
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三九月月考文科数学试卷(解析版) 题型:填空题
已知函数f(x)是(-∞,+∞)上的偶函数,若对于x≥0,都有f(x+2)=f(x),且当x∈[0,2)时,f(x)=log2(x+1),则f(-2012)+f(2013)=________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com