练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设x、y满足约束条件
    x-y+2≥0
    3x-y-2≤0
    x≥0
    y≥0
    ，若目标函数z=ax+by（a＞0，b＞0）的最大值为6，则log3（
    1
    a
    +
    2
    b
    ）的最小值为（　　）
    A、1B、2C、3D、4
    考点：简单线性规划
    专题：不等式的解法及应用
    分析：作出不等式组对应的平面区域，利用目标函数的几何意义，确定z取最大值点的最优解，利用基本不等式的性质，利用数形结合即可得到结论．
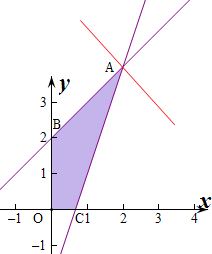    解答： 解：作出不等式组对应的平面区域如图：
    由z=ax+by（a＞0，b＞0）得y=-
    a
    b
    x+
    z
    b
    ，
    则直线的斜率k=-
    b
    a
    ＜0，截距最大时，z也最大．
    平移直y=-
    a
    b
    x+
    z
    b
    ，由图象可知当直线y=-
    a
    b
    x+
    z
    b
    经过点A时，
    直线y=-
    a
    b
    x+
    z
    b
    的截距最大，此时z最大，
    由
    x-y+2=0
    3x-y-2=0
    ，解得
    x=2
    y=4
    ，
    即A（2，4），
    此时z=2a+4b=6，
    即a+2b=3，
    a
    3
    +
    2b
    3
    =1    ，
    ∴
    1
    a
    +
    2
    b
    =（
    1
    a
    +
    2
    b
    ）（
    a
    3
    +
    2b
    3
    ）=
    5
    3
    +
    2a
    3b
    +
    2b
    3a
    ≥
    5
    3
    +2
    2a
    3b
    •
    2b
    3a
    =
    5
    3
    +
    4
    3
    =3，
    当且仅当
    2a
    3b
    =
    2b
    3a
    ，即a=b=1时取等号，
    此时log3（
    1
    a
    +
    2
    b
    ）≥log33=1，
    故选：A
    点评：本题主要考查线性规划的应用，利用z的几何意义先求出最优解是解决本题的关键，利用基本不等式的解法和结合数形结合是解决本题的突破点．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知
    C
    1
    2014
    （x-1）+
    C
    2
    2014
    （x-1）2+…+
    C
    2014
    2014
    （x-1）2014=a0+a1x+a2x2+…+a2014x2014，则a1+a2+…+a2013=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在复平面内，复数z=
    3-4i
    1+3i
    （i为虚数单位）的共轭复数对应的点位于（　　）
    A、第一象限B、第二象限
    C、第三象限D、第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    经统计，用于数学学习的时间（单位：小时）与成绩（单位：分）近似于线性相关关系，对每小组学生每周用于数学的学习时间x与数学成绩y进行数据收集如下：
    x1516181922
    y10298115115120
    由表中样本数据求得回归方程为
    y
    =bx+a，则点（a，b）与直线x+18y=100的位置关系是（　　）
    A、点在直线左侧
    B、点在直线右侧
    C、点在直线上
    D、无法确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=a x2-2bx+1（a＞0，a≠1）在区间（-∞，2]单调递减，且2a+b≤5，则
    b+1
    a+2
    的取值范围为（　　）
    A、（
    6
    7
    ，1）
    B、[
    6
    7
    ，
    4
    3
    ）
    C、[
    6
    7
    ，1]
    D、（
    6
    7
    ，
    4
    3
    ]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面直角坐标系xOy中，设D={（x，y）||x|≤2，|y|≤2}，E={（x，y）|x2+y2≤1}，向D中随机投一点，则所投点在E中的概率是（　　）
    A、
    π
    4
    B、
    π
    16
    C、
    π
    8
    D、
    π2
    16

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    i是虚数单位，
    i
    1-i
    =（　　）
    A、-
    1
    2
    +
    1
    2
    i
    B、
    1
    2
    +
    1
    2
    i
    C、
    1
    2
    -
    1
    2
    i
    D、-
    1
    2
    -
    1
    2
    i

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题中假命题是（　　）
    A、“存在x∈R，使得x2+x+1＜0”的否定是“对任意x∈R，均有x2+x+1≥0”
    B、设随机变量ξ～N（0，1）．若P（ξ≥2）=p．则P（-2＜ξ＜0）=
    1
    2
    -p
    C、若函数y=lg（mx2-x-1）的值域为R，则m＜-
    1
    4
    D、若a＞0，b＞0，a+b=4．则
    1
    a
    +
    2
    b
    的最小值为
    3+2
    		2
    4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    等比数列{an}中，a1=1，a4=8．
    （Ⅰ）求{an}的通项公式；
    （Ⅱ）数列{bn}满足a2，a bn，a2n+2成等比数列，若b1+b2+b3+…+bm≤b10，求正整数m的值．

    查看答案和解析>>

    同步练习册答案