
已知椭圆 的左右顶点分别为
的左右顶点分别为 ,离心率
,离心率 .
.
(1)求椭圆的方程;
(2)若点 为曲线
为曲线 :
: 上任一点(
上任一点( 点不同于
点不同于 ),直线
),直线 与直线
与直线 交于点
交于点 ,
, 为线段
为线段 的中点,试判断直线
的中点,试判断直线 与曲线
与曲线 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014高考名师推荐数学理科二项式定理与性质(解析版) 题型:选择题
对于二项式 ,四位同学作出了四种判断:
,四位同学作出了四种判断:
①存在 ,展开式中有常数项
,展开式中有常数项
②对任意 ,展开式中没有常数项
,展开式中没有常数项
③对任意 ,展开式中没有x的一次项
,展开式中没有x的一次项
④存在 ,展开式中有x的一次项.
,展开式中有x的一次项.
上述判断中正确的是( )
A.①③ B.②③ C.②④ D.①④
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文空间线面平行、面面平行、线面垂直、面面垂直(解析版) 题型:选择题
在正三棱锥P?ABC中,D,E分别是AB,BC的中点,下列结论:①AC⊥PB;②AC∥平面PDE;③AB⊥平面PDE,其中错误的结论个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:解答题
给定抛物线 ,
,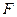 是抛物线
是抛物线 的焦点,过点
的焦点,过点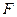 的直线
的直线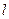 与
与 相交于
相交于 、
、 两点,
两点, 为坐标原点.
为坐标原点.
(1)设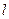 的斜率为1,求以
的斜率为1,求以 为直径的圆的方程;
为直径的圆的方程;
(2)设 ,求直线
,求直线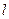 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:解答题
已知数列 满足奇数项
满足奇数项 成等差数列
成等差数列 ,而偶数项
,而偶数项 成等比数列
成等比数列 ,且
,且 ,
, 成等差数列,数列
成等差数列,数列 的前
的前 项和为
项和为 .
.
(1)求通项 ;
;
(2)求 .
.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:解答题
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
API |
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
记某企业每天由空气污染造成的经济损失S(单位:元),空气质量指数API为ω。在区间[0,100]对企业没有造成经济损失;在区间 对企业造成经济损失成直线模型(当API为150时造成的 经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的 经济损失为2000元;
对企业造成经济损失成直线模型(当API为150时造成的 经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的 经济损失为2000元;
(1)试写出是S(ω)的表达式;
(2)试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关?
|
附:

| 非重度污染 | 重度污染 | 合计 |
供暖季 |
|
|
|
非供暖季 |
|
|
|
合计 |
|
| 100 |
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科选择题专项训练(解析版) 题型:选择题
在“魅力中国中学生歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )

A.5和1.6
B.85和1.6
C.85和0.4
D.5和0.4
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科解答题前三题(解析版) 题型:解答题
已知函数 在区间
在区间 上的最大值为2
上的最大值为2 .
.
(1)求常数 的值;
的值;
(2)在 中的角
中的角 ,
, ,
,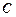 所对的边是
所对的边是 ,
, ,
, ,若
,若
 ,
, 面积为
面积为 . 求边长
. 求边长 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com