已知函数
在区间
上的最大值为2
.
（1）求常数
的值；
（2）在
中的角
,
,
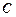所对的边是
,
,
，若
，面积为
. 求边长.
字词句段篇系列答案科目：高中数学 来源：2014高考名师推荐数学文科预测题（解析版） 题型：解答题
已知椭圆
的左右顶点分别为
，离心率
．
（1）求椭圆的方程；
（2）若点
为曲线
:
上任一点（点不同于
），直线
与直线
交于点
，
为线段
的中点，试判断直线
与曲线的位置关系，并证明你的结论．
查看答案和解析>>
科目：高中数学 来源：2014高考名师推荐数学文科运用导数法确定函数的极值、最值、图像（解析版） 题型：选择题
已知
其导函数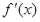
的图象如图，则函数
的极小值是（ ）
A.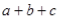 
B. 
C. 
D. c
查看答案和解析>>
科目：高中数学 来源：2014高考名师推荐数学文科解答题后三题（解析版） 题型：解答题
已知椭圆
的中心在坐标原点，焦点在
轴上，离心率为
，椭圆上的点到焦点距离的最大值为
．
（1）求椭圆的标准方程；
（2）若过点
的直线
与椭圆交于不同的两点
，且
，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源：2014高考名师推荐数学文科解答题前三题（解析版） 题型：解答题
如图，已知四棱锥P-ABCD的底面ABCD是菱形，且PC⊥平面ABCD，PC＝AC＝2,E是PA的中点。
(1)求证：AC⊥平面BDE；
(2)若直线PA与平面PBC所成角为30°，求二面角P-AD-C的正切值；
(3)求证：直线PA与平面PBD所成的角φ为定值，并求sinφ值。
查看答案和解析>>
科目：高中数学 来源：2014高考名师推荐数学文科解三角形（解析版） 题型：选择题
在△ABC中，内角A、B、C的对边分别为a、b、c，且
，则△ABC是( )
A. 钝角三角形
B. 直角三角形
C. 锐角三角形
D. 等边三角形
查看答案和解析>>
科目：高中数学 来源：2014高考名师推荐数学文科角的集合表示（解析版） 题型：选择题
集合P＝{x|2kπ≤α≤(2k＋1)π，k∈Z}，Q＝{α|－4≤α≤4}．则P∩Q＝( )
A. 
B. {α|－4≤α≤－π或0≤α≤π}
C. {α|－4≤α≤4}
D. {α|0≤α≤π}
查看答案和解析>>
科目：高中数学 来源：2014高考名师推荐数学文科线性回归方程（解析版） 题型：选择题
一台机器由于使用时间较长，但还可以使用，它按不同的转速生产出来的某机器零件有一些会有缺点，每小时生产有缺点零件的多少随机器运转的速度而变化，下表是抽样试验结果：
转速x/(rad/s) | 16 | 14 | 12 | 8 |
每小时生产有缺点的零件数y/件 | 11 | 9 | 8 | 5 |
若实际生产中，允许每小时的产品中有缺点的零件数最多为10个，那么机器的转速应该控制所在的范围是（ ）
A.10转/s以下
B.15转/s以下
C.20转/s以下
D.25转/s以下
查看答案和解析>>
科目：高中数学 来源：2014高考名师推荐数学文科直线与圆锥曲线（解析版） 题型：选择题
椭圆
的右焦点为
，椭圆
与
轴正半轴交于
点，与
轴正半轴交于
，且
，过点
作直线
交椭圆于不同两点
,则直线的斜率的取值范围是（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
（2）
∴
在区间
上是增函数，在区间
上是减函数 ∴当
即
时，函数
在区间
上取到最大值.
得
∴ 
∴ 
，解得
(舍去)或
∵ 
，
∴ 
…………①
面积为
即
…………②
