
如图,已知四棱锥P-ABCD的底面ABCD是菱形,且PC⊥平面ABCD,PC=AC=2,E是PA的中点。
(1)求证:AC⊥平面BDE;
(2)若直线PA与平面PBC所成角为30°,求二面角P-AD-C的正切值;
(3)求证:直线PA与平面PBD所成的角φ为定值,并求sinφ值。

(1)见解析 (2) tan∠PDC =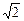 (3) sinφ=
(3) sinφ=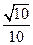
【解析】(1)设CA与BD相交于O,连EO,
由底面ABCD是菱形得O是中点,且CA⊥BD,
E是PA的中点,得OE//PC
∵ PC⊥平面ABCD,∴OE⊥平面ABCD
∴ OE⊥AC
∴ AC⊥面BDE
(2)由上知,建立如图坐标系,设BD=2a;
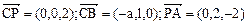
设平面的法向量为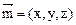
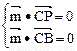 ,令x=1得
,令x=1得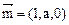
由题意PA与面PBC所成角为30°,得: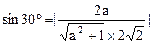 得a=1。
得a=1。
解法一:当a=1时,底面ABCD是正方形,AD⊥CD
∵ PC⊥平面ABCD
∴ PC⊥AD
∴ AD⊥面PCD
则PD⊥AD
∠PDC是二面角P-AD-C的平面角,且tan∠PDC =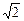 解法二:当a=1时,
解法二:当a=1时,
面ACD的法向量为(0,0,1),设面PAD的法向量为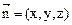
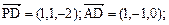
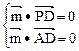 令x=1,则
令x=1,则
二面角P-AD-C的平面角为锐角θ,cosθ= ,tanθ=
,tanθ=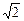 (3)设面PBD的法向量为
(3)设面PBD的法向量为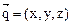
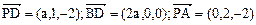
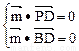 令z=1得
令z=1得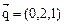
则sinφ=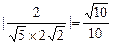 为定值。
为定值。


科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:解答题
已知数列 满足奇数项
满足奇数项 成等差数列
成等差数列 ,而偶数项
,而偶数项 成等比数列
成等比数列 ,且
,且 ,
, 成等差数列,数列
成等差数列,数列 的前
的前 项和为
项和为 .
.
(1)求通项 ;
;
(2)求 .
.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科运用导数解决实际问题(解析版) 题型:选择题
把一个周长为12cm的长方形围成一个圆柱,当圆柱的体积最大时,该圆柱底面周长与高的比为( )
A. 1:2
B. 1:π
C. 2:1
D. 2:π
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科解答题后三题(解析版) 题型:解答题
设椭圆C1和抛物线C2的焦点均在 轴上,C1的中心和C2的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表中:
轴上,C1的中心和C2的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表中:
| 3 | -2 | 4 |
|
|
| 0 | -4 |
|
(1)求曲线C1,C2的标准方程;
(2)设直线 与椭圆C1交于不同两点M、N,且
与椭圆C1交于不同两点M、N,且 。请问是否存在直线
。请问是否存在直线 过抛物线C2的焦点F?若存在,求出直线
过抛物线C2的焦点F?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科解答题后三题(解析版) 题型:解答题
已知双曲线 =1
=1  的两个焦点为
的两个焦点为 、
、 ,P是双曲线上的一点,
,P是双曲线上的一点,
且满足  ,
,
(1)求 的值;
的值;
(2)抛物线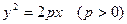 的焦点F与该双曲线的右顶点重合,斜率为1的直线经过点F与该抛物线交于A、B两点,求弦长|AB|.
的焦点F与该双曲线的右顶点重合,斜率为1的直线经过点F与该抛物线交于A、B两点,求弦长|AB|.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科解答题前三题(解析版) 题型:解答题
已知函数 在区间
在区间 上的最大值为2
上的最大值为2 .
.
(1)求常数 的值;
的值;
(2)在 中的角
中的角 ,
, ,
, 所对的边是
所对的边是 ,
, ,
, ,若
,若
 ,
, 面积为
面积为 . 求边长
. 求边长 .
.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科线性规划(解析版) 题型:选择题
某旅行社租用A、B两种型号的客车安排900名客人旅行,A、B两种车辆的载客量分别为36人和60人,租金分别为1600元/辆和2400元/辆,旅行社要求租车总数不超过21辆,且B型车不多于A型车7辆.则租金最少为 是( )
A. 31200元
B. 36000元
C. 36800元
D. 38400元
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科直线与圆锥曲线(解析版) 题型:选择题
已知(4,2)是直线l被椭圆 所截得的线段的中点,则l的方程是( )
所截得的线段的中点,则l的方程是( )
A.x+2y+8=0
B.x+2y-8=0
C.x-2y-8=0
D.x-2y+8=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com