设椭圆C1和抛物线C2的焦点均在
轴上，C1的中心和C2的顶点均为原点，从每条曲线上各取两点，将其坐标记录于下表中：
| 3 | -2 | 4 |
|
|
| 0 | -4 |
|
（1）求曲线C1，C2的标准方程；
（2）设直线
与椭圆C1交于不同两点M、N，且
。请问是否存在直线过抛物线C2的焦点F？若存在，求出直线的方程；若不存在，请说明理由.
科目：高中数学 来源：2014高考名师推荐数学文科预测题（解析版） 题型：解答题
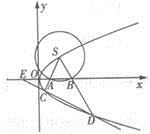
如图，
是抛物线为
上的一点，以S为圆心，r为半径（
）做圆，分别交x轴于A，B两点，连结并延长SA、SB，分别交抛物线于C、D两点。
（1）求证：直线CD的斜率为定值；
（2）延长DC交x轴负半轴于点E，若EC : ED = 1 : 3，求
的值。
查看答案和解析>>
科目：高中数学 来源：2014高考名师推荐数学文科运用导数法确定函数的极值、最值、图像（解析版） 题型：选择题
已知
其导函数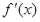
的图象如图，则函数
的极小值是（ ）
A.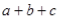 
B. 
C. 
D. c
查看答案和解析>>
科目：高中数学 来源：2014高考名师推荐数学文科解答题后三题（解析版） 题型：解答题
已知椭圆
的中心在坐标原点，焦点在
轴上，离心率为
，椭圆上的点到焦点距离的最大值为
．
（1）求椭圆的标准方程；
（2）若过点
的直线
与椭圆交于不同的两点
，且
，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源：2014高考名师推荐数学文科解答题前三题（解析版） 题型：解答题
如图，已知四棱锥P-ABCD的底面ABCD是菱形，且PC⊥平面ABCD，PC＝AC＝2,E是PA的中点。
(1)求证：AC⊥平面BDE；
(2)若直线PA与平面PBC所成角为30°，求二面角P-AD-C的正切值；
(3)求证：直线PA与平面PBD所成的角φ为定值，并求sinφ值。
查看答案和解析>>
科目：高中数学 来源：2014高考名师推荐数学文科角的集合表示（解析版） 题型：选择题
集合P＝{x|2kπ≤α≤(2k＋1)π，k∈Z}，Q＝{α|－4≤α≤4}．则P∩Q＝( )
A. 
B. {α|－4≤α≤－π或0≤α≤π}
C. {α|－4≤α≤4}
D. {α|0≤α≤π}
查看答案和解析>>
科目：高中数学 来源：2014高考名师推荐数学文科空间直角坐标系简单应用（解析版） 题型：选择题
已知点A(1，－2，11)，B(4，2，3)，C(6，－1，4)，则△ABC的形状是( )
A．锐角三角形
B．钝角三角形
C．直角三角形
D．等边三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
；
，则
.
椭圆C1上任何点的横坐标
也在C1上，从而
，
C1的方程为
，（4，-4）一定在C2上，设C2的方程为
即C2的方程为
过C2的焦点F（1，0）。当
，与已知矛盾。 当
，则
代入C1方程并整理得：
设
，则
，
，
在区间[0,1]上的最小值等于-3，则实数
的取值范围是 ( )
B.
D.
的取值范围是 ( )
