
已知椭圆 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,离心率为
轴上,离心率为 ,椭圆
,椭圆 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若过点 的直线
的直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:解答题
给定抛物线 ,
,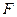 是抛物线
是抛物线 的焦点,过点
的焦点,过点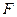 的直线
的直线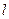 与
与 相交于
相交于 、
、 两点,
两点, 为坐标原点.
为坐标原点.
(1)设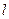 的斜率为1,求以
的斜率为1,求以 为直径的圆的方程;
为直径的圆的方程;
(2)设 ,求直线
,求直线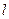 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科选择题专项训练(解析版) 题型:选择题
在“魅力中国中学生歌手大赛”比赛现场上七位评委为某选手打出的分数的茎叶统计图如图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )

A.5和1.6
B.85和1.6
C.85和0.4
D.5和0.4
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科证明不等式(解析版) 题型:选择题
设m>n,n∈N+,x>1,a=(lgx)m+(lgx)-m,b=(lgx)n+(lgx)-n,则a与b的大小关系为( )
A. a≥b
B. a≤b
C. 与x的值有关,大小不定
D. 以上都不正确
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科解答题后三题(解析版) 题型:解答题
设椭圆C1和抛物线C2的焦点均在 轴上,C1的中心和C2的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表中:
轴上,C1的中心和C2的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表中:
| 3 | -2 | 4 |
|
|
| 0 | -4 |
|
(1)求曲线C1,C2的标准方程;
(2)设直线 与椭圆C1交于不同两点M、N,且
与椭圆C1交于不同两点M、N,且 。请问是否存在直线
。请问是否存在直线 过抛物线C2的焦点F?若存在,求出直线
过抛物线C2的焦点F?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科解答题前三题(解析版) 题型:解答题
已知向量a=(cosωx,sinωx),b=(cosωx, cosωx),其中0<ω<2,函数
cosωx),其中0<ω<2,函数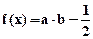 ,其图象的一条对称轴为
,其图象的一条对称轴为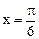 。
。
(1)求函数的表达式及单调递增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,S△ABC为其面积,若 ,b=1,
,b=1, ,求a的值。
,求a的值。
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科解答题前三题(解析版) 题型:解答题
已知函数 在区间
在区间 上的最大值为2
上的最大值为2 .
.
(1)求常数 的值;
的值;
(2)在 中的角
中的角 ,
, ,
,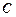 所对的边是
所对的边是 ,
, ,
, ,若
,若
 ,
, 面积为
面积为 . 求边长
. 求边长 .
.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科绝对值不等式(解析版) 题型:选择题
若关于x的不等式|x-2|+|x-a|≥a在R上恒成立,则a的最大值是( )
A. 0
B. 1
C. -1
D. 2
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科空间垂直、平行关系(解析版) 题型:选择题
如图所示,正方体 的棱长为a,M、N分别为
的棱长为a,M、N分别为 和AC上的点,
和AC上的点, ,则MN与平面
,则MN与平面 的位置关系是( )
的位置关系是( )

A.相交 B.平行 C.垂直 D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com