练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知双曲线=1 的两个焦点为、，P是双曲线上的一点，

    且满足  ，

    （1）求的值；

    （2）抛物线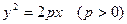的焦点F与该双曲线的右顶点重合，斜率为1的直线经过点F与该抛物线交于A、B两点，求弦长|AB|.

     

    (1) (2)16

    【解析】（1）根据题意，

    又，，，又|P F|•|PF|=| FF|=，  |P F|<4， 得在区间（0,4）上有解， 所以

    因此，又，所以

    （2）双曲线方程为=1，右顶点坐标为（2,0），即

    所以抛物线方程为     直线方程为

    由（1）（2）两式联立，解得和

    所以弦长|AB|==16

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014高考名师推荐数学文科预测题（解析版） 题型：填空题

    如图，AB是⊙O的一条切线，切点为B，ADE、CFD都是⊙O的割线，AC=AB.

    （1）证明：AC2=AD·AE

    （2）证明：FG∥AC

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科选择题专项训练（解析版） 题型：选择题

    已知平面向量，满足，，与的夹角为，若，则实数的值为（     ）

    A.1 B. C.2 D.3

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科证明不等式（解析版） 题型：选择题

    已知△ABC中,∠C=90°,则的取值范围是　(　　)

    A. (0,2)

    B.

    C.

    D.

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科解答题后三题（解析版） 题型：解答题

    已知函数．

    （1）当时函数取得极小值，求a的值；（2）求函数的单调区间．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科解答题前三题（解析版） 题型：解答题

    如图，已知四棱锥P-ABCD的底面ABCD是菱形，且PC⊥平面ABCD，PC＝AC＝2,E是PA的中点。

    (1)求证：AC⊥平面BDE；

    (2)若直线PA与平面PBC所成角为30°，求二面角P-AD-C的正切值；

    (3)求证：直线PA与平面PBD所成的角φ为定值，并求sinφ值。

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科解答题前三题（解析版） 题型：解答题

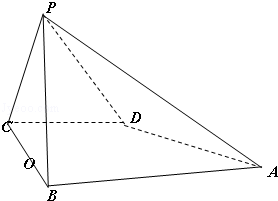
    如图，已知四棱锥P﹣ABCD的底面是直角梯形，∠ABC=∠BCD=90°，AB=BC=2CD=2，PB=PC=3，侧面PBC⊥底面ABCD，O是BC的中点．

    （1）求证：DC∥平面PAB；

    （2）求四棱锥P﹣ABCD的体积．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科绝对值不等式（解析版） 题型：选择题

    若关于x的不等式|a|≥|x＋1|＋|x－2|存在实数解，则实数a的取值范围是(　　)

    A. [3，+∞)

    B. (－∞，3]

    C. (-1,2)

    D. (-2,3]

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科相互独立事件（解析版） 题型：选择题

    若事件A和B是相互独立事件,且P（A·B）＝0.48,P（A·B）＝0.08,P（A）＞P（B）,则P（A）的值为（    ）

    A.0.5 B.0.6 C.0.8 D.0.9

     

    查看答案和解析>>

    同步练习册答案