练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
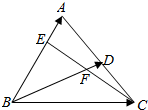
    14．如图，在△ABC中，D为AC的中点，E是AB上的点，且$\frac{AE}{EB}$=$\frac{1}{2}$，CE和BD交于点F，设$\overrightarrow{BD}$=$\overrightarrow{a}$，$\overrightarrow{BA}$=$\overrightarrow{b}$．
    （1）用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{BC}$，$\overrightarrow{EC}$；
    （2）求$\frac{BF}{FD}$的值．

    分析 （1）由$\overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BD}$得$\overrightarrow{BC}$=2$\overrightarrow{BD}$-$\overrightarrow{BA}$=2$\overrightarrow{a}$-$\overrightarrow{b}$；$\overrightarrow{EC}$=$\overrightarrow{EA}+\overrightarrow{AC}$=$\overrightarrow{EA}+2\overrightarrow{AD}$；
    （2）设$\overrightarrow{EF}=λ$$\overrightarrow{EC}$，求出$\overrightarrow{BF}$，由B，F，D三点共线得$\overrightarrow{BF}$=k$\overrightarrow{BD}$，列方程解出λ，k，得到$\frac{BF}{FD}$的值．

    解答 解：（1）∵D是AC的中点，∴$\overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BD}$，∴$\overrightarrow{BC}$=2$\overrightarrow{BD}$-$\overrightarrow{BA}$=2$\overrightarrow{a}$-$\overrightarrow{b}$；
    ∵$\frac{AE}{EB}$=$\frac{1}{2}$，∴$\overrightarrow{EA}$=$\frac{1}{3}\overrightarrow{BA}$=$\frac{1}{3}\overrightarrow{b}$，∵$\overrightarrow{AD}$=$\overrightarrow{BD}-\overrightarrow{BA}$=$\overrightarrow{a}-\overrightarrow{b}$，∴$\overrightarrow{EC}$=$\overrightarrow{EA}+\overrightarrow{AC}$=$\overrightarrow{EA}+2\overrightarrow{AD}$=2$\overrightarrow{a}$-$\frac{5}{3}$$\overrightarrow{b}$．
    （2）设$\overrightarrow{EF}=λ$$\overrightarrow{EC}$=2λ$\overrightarrow{a}$-$\frac{5λ}{3}$$\overrightarrow{b}$，则$\overrightarrow{BF}$=$\overrightarrow{BE}+\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{b}$+2λ$\overrightarrow{a}$-$\frac{5λ}{3}$$\overrightarrow{b}$=2λ$\overrightarrow{a}$+$\frac{2-5λ}{3}$$\overrightarrow{b}$．
    ∵B，F，D三点共线，∴$\overrightarrow{BF}$=k$\overrightarrow{BD}$=k$\overrightarrow{a}$，∴$\left\{\begin{array}{l}{2λ=k}\\{\frac{2-5λ}{3}=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{λ=\frac{2}{5}}\\{k=\frac{4}{5}}\end{array}\right.$．
    ∴$\overrightarrow{BF}=\frac{4}{5}\overrightarrow{BD}$，∴$\frac{BF}{FD}$=4．

    点评 本题考查了平面向量的基本定理，三点共线原理的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．下列命题中正确的个数为（　　）
    ①若“一个整数的末位数字是0，则这个整数能被5整除”的逆命题；
    ②若“一个三角形有两条边相等，则这个三角形有两个角相等”的否命题；
    ③“奇函数的图象关于原点对称”的逆否命题；
    ④“每个正方形都是平行四边形”的否定；
    ⑤设a，b∈R，则“a＞b”是“a|a|＞b|b|”的充分不必要条件．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．发现有一批不锈钢材料，可用于绿地围边，经测算可围长度为200米，现选如图所示4块同样大小的长方形绿地，四周用不锈钢围边，中间用不锈钢隔开．问如何设计所围绿地总面积最大？最大总面积为多少平方米？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知三棱锥P-ABC的四个顶点都在球O的表面上，且PA=PB=PC=2$\sqrt{5}$，若平面ABC被球O截得的截面面积为16π，则球O的表面积为100π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知点（b，$\sqrt{2}$a）在双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）上，则双曲线C的渐近线方程为（　　）
    A．x=±$\sqrt{2}$yB．y=±$\sqrt{2}$xC．y=±2xD．x=±2y

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．设数列{an}中，a1=1，an=$\frac{n+1}{n-1}$an-1，则通项公式an=$\frac{n（n+1）}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．数列6，0，6，0，…的一个通项公式是an=3+3•（-1）n+1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．设函数f（x）定义域为[0，1]，若f（x）在[0，x*]上单调递增，在[x*，1]上单调递减，则称x*为函数f（x）的峰点，f（x）为含峰函数．（特别地，若f（x）在[0，1]上单调递增或递减，则峰点为1或0）
    对于不易直接求出峰点x*的含峰函数，可通过做试验的方法给出x*的近似值．试验原理为：“对任意的x1，x2∈（0，1），x1＜x2，若f（x1）≥f（x2），则（0，x2）为含峰区间，此时称x1为近似峰点；若f（x1）＜f（x2），则（x1，1）为含峰区间，此时称x2为近似峰点”．
    我们把近似峰点与x*之间可能出现的最大距离称为试验的“预计误差”，记为d，其值为d=max{max{x1，x2-x1}，max{x2-x1，1-x2}}（其中max{x，y}表示x，y中较大的数）．
    （Ⅰ）若x1=$\frac{1}{4}$，x2=$\frac{1}{2}$．求此试验的预计误差d．
    （Ⅱ）如何选取x1、x2，才能使这个试验方案的预计误差达到最小？并证明你的结论（只证明x1的取值即可）
    （Ⅲ）选取x1，x2∈（0，1），x1＜x2，可以确定含峰区间为（0，x2）或（x1，1）．在所得的含峰区间内选取x3，由x3与x1或x3与x2类似地可以进一步得到一个新的预计误差d′．分别求出当x1=$\frac{1}{4}$和x1=$\frac{2}{5}$时预计误差d′的最小值．（本问只写结果，不必证明）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．命题“?x∈R，x2-1＞0”的否定是（　　）
    A．?x∈R，x2-1≤0B．?x0∈R，x02-1＞0C．?x0∈R，x02-1≤0D．?x∈R，x2-1＜0

    查看答案和解析>>

    同步练习册答案