
分析 (Ⅰ)通过代入联立$\root{3}{2}≤x≤8$、$\root{3}{x}≤27≤{x^3}$可得结论;
(Ⅱ)通过换元令bn=lgan、设Sn=lgb1+…+lgbn,则问题转化为:若$\frac{1}{3}{S_n}≤{S_{n+1}}≤3{S_n}$,求p的范围.利用$\frac{1}{3}{b_1}≤{b_2}≤3{b_1}$可知$\frac{1}{3}≤p≤3$.进而分p=1、1<p≤3、$\frac{1}{3}≤p<1$三种情况讨论即可;
(Ⅲ)通过令${c_n}={log_{\frac{3}{2}}}{a_n}$,可知{cn}是首项为1、公差为$d={log_{\frac{3}{2}}}q$的等差数列,进而取特殊值确定kmax≥1000,转化为不等式问题计算即得结论.
解答 解:(Ⅰ)依题意,$\root{3}{a_2}≤{a_3}≤a_2^3$,
因为a2=2,a3=x,所以$\root{3}{2}≤x≤8$,
又因为a4=27,$\root{3}{a_3}≤{a_4}≤a_3^3$,所以$\root{3}{x}≤27≤{x^3}$,
综上可得3≤x≤8;
(Ⅱ)令bn=lgan,则bn是公比为p的等比数列,$\frac{1}{3}{b_n}≤{b_{n+1}}≤3{b_n}$,
设Sn=lgb1+…+lgbn,则问题转化为:若$\frac{1}{3}{S_n}≤{S_{n+1}}≤3{S_n}$,求p的范围.
由已知得${b_n}={b_1}{q^{n-1}}$=qn-1•$lg\frac{3}{2}$,又$\frac{1}{3}{b_1}≤{b_2}≤3{b_1}$,所以$\frac{1}{3}≤p≤3$.
(1)当p=1时,Sn=n,$\frac{1}{3}{S_n}≤{S_{n+1}}≤3{S_n}$,即$\frac{n}{3}≤n+1≤3n$,成立;
(2)当1<p≤3时,${S_n}={b_1}\frac{{{p^n}-1}}{p-1}$,$\frac{1}{3}{S_n}≤{S_{n+1}}≤3{S_n}$,即$\frac{1}{3}\frac{{{p^n}-1}}{p-1}≤\frac{{{p^{n+1}}-1}}{p-1}≤3\frac{{{p^n}-1}}{p-1}$,
∴$\frac{1}{3}≤\frac{{{p^{n+1}}-1}}{{{p^n}-1}}≤3$,此不等式即$\left\{{\begin{array}{l}{3{p^{n+1}}-{p^n}-2≥0}\\{{p^{n+1}}-3{p^n}+2≤0}\end{array}}\right.$,
∵p>1,∴3pn+1-pn-2=pn(3p-1)-2>2pn-2>0,
对于不等式pn+1-3pn+2≤0,令n=1,得p2-3p+2≤0,解得1≤p≤2,
又当1<p≤2时,p-3<0,∴pn+1-3pn+2=pn(p-3)+2≤p(p-3)+2=(p-1)(p-2)≤0成立,
所以1<p≤2;
(3)当$\frac{1}{3}≤p<1$时,${S_n}={b_1}\frac{{1-{p^n}}}{1-p}$,$\frac{1}{3}{S_n}≤{S_{n+1}}≤3{S_n}$,即$\frac{1}{3}\frac{{1-{p^n}}}{1-p}≤\frac{{1-{p^{n+1}}}}{1-p}≤3\frac{{1-{p^n}}}{1-p}$,
即$\left\{{\begin{array}{l}{3{p^{n+1}}-{p^n}-2≤0}\\{{p^{n+1}}-3{p^n}+2≥0}\end{array}}\right.$,3p-1>0,p-3<0,
∵3pn+1-pn-2=qn(3q-1)-2<2qn-2<0pn+1-3pn+2=pn(p-3)+2≥p(p-3)+2=(p-1)(p-2)>0,
∴$\frac{1}{3}≤p<1$时,不等式恒成立.
综上,q的取值范围为$\frac{1}{3}≤p≤2$.
(Ⅲ)令${c_n}={log_{\frac{3}{2}}}{a_n}$,则cn是首项为1,公差为$d={log_{\frac{3}{2}}}q$的等差数列,
满足c1+c2+…+ck=1000.显然,当k=1000,d=0时,是一组符合题意的解,∴kmax≥1000,
则由已知得$\frac{1+(k-2)d}{3}≤1+(k-1)d≤3[1+(k-2)d]$,
∴$\left\{{\begin{array}{l}{(2k-1)d≥-2}\\{(2k-5)d≥-2}\end{array}}\right.$,当k≥1000时,不等式即$d≥-\frac{2}{2k-1},d≥-\frac{2}{2k-5}$,
∴$d≥-\frac{2}{2k-1}$,${a_1}+{a_2}+…+{a_k}=k+\frac{k(k-1)d}{2}=1000$,
∴k≥1000时,$d=\frac{2000-2k}{k(k-1)}≥-\frac{2}{2k-1}$,
解得$1000-\sqrt{999000}≤k≤1000+\sqrt{999000}$,∴k≤1999,
∴k的最大值为1999,此时公差$d=\frac{2000-2k}{k(k-1)}=-\frac{1998}{1999×1998}=-\frac{1}{1999}$,
此时公比$q={(\frac{3}{2})^{-\frac{1}{1999}}}$.
点评 本题考查是一道关于数列与不等式的综合题,涉及最值问题,考查分类讨论的思想,考查转化思想,考查运算求解能力,注意解题方法的积累,属于难题.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
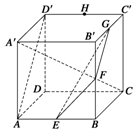 在正方体ABCD-A′B′C′D′中,棱AB,BB′,B′C′,C′D′的中点分别是E,F,G,H,如图所示.
在正方体ABCD-A′B′C′D′中,棱AB,BB′,B′C′,C′D′的中点分别是E,F,G,H,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 既不是奇函数又不是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com