
分析 由题意可得当x=$\frac{1}{2}$时,4x =log2ax,由此求得a的值.
解答 解:∵关于x的不等式4x<log2ax(a>0,且a≠$\frac{1}{2}$)的解集是{x|0<x<$\frac{1}{2}$},
则当x=$\frac{1}{2}$时,4x =log2ax,即 2=log2a$\frac{1}{2}$,∴(2a)2=$\frac{1}{2}$,∴2a=$\frac{\sqrt{2}}{2}$,∴a=$\frac{\sqrt{2}}{4}$,
故答案为:$\left\{{\frac{{\sqrt{2}}}{4}}\right\}$.
点评 本题主要考查指数不等式、对数不等式的解法,体现了转化的数学思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
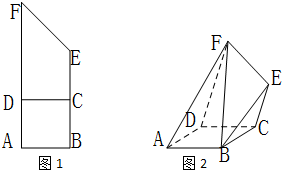 直角梯形ABEF中,BE∥AF,∠FAB=90°,AF=$\frac{3}{2}$BE=3AB=3,C,D分别是边BE,AF上的点(不是端点),且CD⊥AF,如图1所示;现沿CD把直角梯形ABEF折成一个120°的二面角,连接部分线段后围成一个空间几何体,如图2所示.
直角梯形ABEF中,BE∥AF,∠FAB=90°,AF=$\frac{3}{2}$BE=3AB=3,C,D分别是边BE,AF上的点(不是端点),且CD⊥AF,如图1所示;现沿CD把直角梯形ABEF折成一个120°的二面角,连接部分线段后围成一个空间几何体,如图2所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\overrightarrow a-\frac{1}{2}\overrightarrow b$ | B. | $-\overrightarrow a+\frac{1}{2}\overrightarrow b$ | C. | $\overrightarrow a-\frac{1}{2}\overrightarrow b$ | D. | $\overrightarrow a+\frac{1}{2}\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{7}{10}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-3)2+(y+1)2=4 | B. | (x-1)2+(y-1)2=4或(x+1)2+(y+1)2=4 | ||
| C. | (x+3)2+(y-1)2=4 | D. | (x+1)2+(y-1)2=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
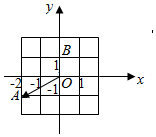 如图,在复平面内,复数z1,z2对应的向量分别为$\overrightarrow{OA}$,$\overrightarrow{OB}$,则复数$\overline{z_1}$+2z2=( )?
如图,在复平面内,复数z1,z2对应的向量分别为$\overrightarrow{OA}$,$\overrightarrow{OB}$,则复数$\overline{z_1}$+2z2=( )?| A. | -2+i | B. | -2+3i | C. | 1+2i | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 31 | C. | -33 | D. | -31 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com