
| A. | (0,+∞) | B. | [2,+∞) | C. | (-∞,2] | D. | (0,2] |
分析 由题意:函数f(x)=(${\frac{1}{2}}$)${\;}^{{x^2}-2x}}$是复合函数,令x2-2x=t可得出函数f(x)=$(\frac{1}{2})^{t}$是减函数,由单调性即可求值域.
解答 解:由题意:函数f(x)=(${\frac{1}{2}}$)${\;}^{{x^2}-2x}}$是复合函数,
令x2-2x=t
则:函数f(x)=$(\frac{1}{2})^{t}$是减函数,
∵x2-2x=t的值域为[-1,+∞)
∴当t=-1时,
函数f(x)=$(\frac{1}{2})^{t}$取得最大值为2;
∴函数f(x)=(${\frac{1}{2}}$)${\;}^{{x^2}-2x}}$的值域为(0,2].
故选D.
点评 本题考查了指数函数的单调性和复合函数的值域的求法.属于中档题.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠ADC=45°,AD=
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠ADC=45°,AD=查看答案和解析>>
科目:高中数学 来源: 题型:解答题
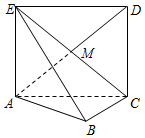 如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC=2
如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC=2查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\frac{{(x-1)({x^4}-3{x^2})}}{x-1}$ | B. | f(x)=x3-2x | ||
| C. | $f(x)=\frac{{{x^2}+1}}{x}$ | D. | f(x)=x2+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com