
【题目】冬季历来是交通事故多发期,面临着货运高危运行、恶劣天气频发、包车客运监管漏洞和农村交通繁忙等四个方面的挑战.全国公安交管部门要认清形势、正视问题,针对近期事故暴露出来的问题,强薄羽、补短板、堵漏洞,进一步推动五大行动,巩固扩大五大行动成果,全力确保冬季交通安全形势稳定.据此,某网站推出了关于交通道路安全情况的调查,通过调查年龄在![]() 的人群,数据表明,交通道路安全仍是百姓最为关心的热点,参与调查者中关注此类问题的约占80%,现从参与调查并关注交通道路安全的人群中随机选出100人,并将这100人按年龄分组:第1组
的人群,数据表明,交通道路安全仍是百姓最为关心的热点,参与调查者中关注此类问题的约占80%,现从参与调查并关注交通道路安全的人群中随机选出100人,并将这100人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
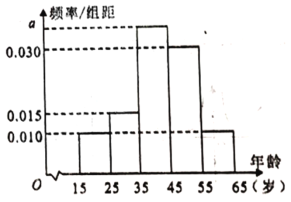
(1)求这100人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(2)现在要从年龄较大的第4,5组中用分层抽样的方法抽取8人,再从这8人中随机抽取3人进行问卷调查,求第4组恰好抽到2人的概率;
(3)若从所有参与调查的人(人数很多)中任意选出3人,设其中关注交通道路安全的人数为随机变量X,求X的分布列与数学期望.
【答案】(1)平均数为![]() 岁;中位数为
岁;中位数为![]() 岁(2)
岁(2)![]() (3)详见解析
(3)详见解析
【解析】
(1)由频率分布直方图能求出![]() ,由此能求出这
,由此能求出这![]() 人年龄的样本平均数和中位数;
人年龄的样本平均数和中位数;
(2)第4,5组抽取的人数分别为6人,2人,设第4组中恰好抽取2人的事件为![]() ,利用排列组合能求出事件
,利用排列组合能求出事件![]() 的概率;
的概率;
(3)从所有参与调查的人中任意选出1人,关注交通道路安全的概率为![]() ,
,![]() 的所有可能取值为0,1,2,3,
的所有可能取值为0,1,2,3,![]() ,分别求出相应的概率,由此能求出
,分别求出相应的概率,由此能求出![]() 的分布列和数学期望.
的分布列和数学期望.
解:(1)由![]() ,得
,得![]() ,
,
平均数为![]() 岁;
岁;
设中位数为x,则![]() ,∴
,∴![]() 岁.
岁.
(2)第4,5组抽取的人数分别为6人,2人.
设第4组中恰好抽取2人的事件为A,则![]() .
.
(3)从所有参与调查的人中任意选出1人,关注交通道路安全的概率为![]() ,
,
X的所有可能取值为0,1,2,3,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
所以X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
∵![]() ,∴
,∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设![]() 为实数,函数
为实数,函数![]() .
.
(1)若函数![]() 是偶函数,求实数
是偶函数,求实数![]() 的值;
的值;
(2)若![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(3)对于函数![]() ,在定义域内给定区间
,在定义域内给定区间![]() ,如果存在
,如果存在![]() ,满足
,满足![]() ,则称函数
,则称函数![]() 是区间
是区间![]() 上的“平均值函数”,
上的“平均值函数”,![]() 是它的一个“均值点”.如函数
是它的一个“均值点”.如函数![]() 是
是![]() 上的平均值函数,
上的平均值函数,![]() 就是它的均值点.现有函数
就是它的均值点.现有函数![]() 是区间
是区间![]() 上的平均值函数,求实数
上的平均值函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若动点![]() 到定点
到定点![]() 与定直线
与定直线![]() 的距离之和为4.
的距离之和为4.
(1)求点![]() 的轨迹方程,并画出方程的曲线草图;
的轨迹方程,并画出方程的曲线草图;
(2)记(1)得到的轨迹为曲线![]() ,问曲线
,问曲线![]() 上关于点
上关于点![]() (
(![]() )对称的不同点有几对?请说明理由.
)对称的不同点有几对?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,侧面
为矩形,侧面![]() 为正三角形,
为正三角形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 为棱
为棱![]() 上一点(不与
上一点(不与![]() 、
、![]() 重合),平面
重合),平面![]() 交棱
交棱![]() 于点
于点![]() .
.
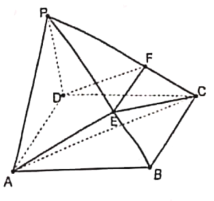
(1)求证:![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冬季历来是交通事故多发期,面临着货运高危运行、恶劣天气频发、包车客运监管漏洞和农村交通繁忙等四个方面的挑战.全国公安交管部门要认清形势、正视问题,针对近期事故暴露出来的问题,强薄羽、补短板、堵漏洞,进一步推动五大行动,巩固扩大五大行动成果,全力确保冬季交通安全形势稳定.据此,某网站推出了关于交通道路安全情况的调查,通过调查年龄在![]() 的人群,数据表明,交通道路安全仍是百姓最为关心的热点,参与调查者中关注此类问题的约占80%.现从参与调查并关注交通道路安全的人群中随机选出100人,并将这100人按年龄分组:第1组
的人群,数据表明,交通道路安全仍是百姓最为关心的热点,参与调查者中关注此类问题的约占80%.现从参与调查并关注交通道路安全的人群中随机选出100人,并将这100人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
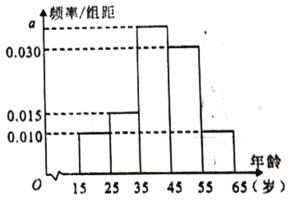
(1)求这100人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(2)现在要从年龄较大的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取2人进行问卷调查,求第2组恰好抽到1人的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且点
,且点![]()
![]() 在函数
在函数![]() 的图像上;
的图像上;
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足:
满足:![]() ,
,![]() ,求
,求![]() 的通项公式;
的通项公式;
(3)在第(2)问的条件下,若对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 满足
满足![]() ,
,![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)若![]() ,数列
,数列![]() 满足关系式
满足关系式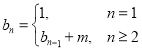 ,求证:数列
,求证:数列![]() 的通项公式为
的通项公式为![]() ;
;
(3)设(2)中的数列![]() 的前n项和为
的前n项和为![]() ,对任意的正整数n,
,对任意的正整数n,![]() 恒成立,求实数p的取值范围.
恒成立,求实数p的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com