
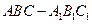 中,平面
中,平面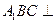 侧面。
侧面。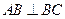 ;
;
 ,证明见解析。
,证明见解析。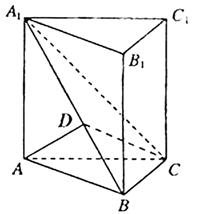
 侧面A1ABB1=A1B,得
侧面A1ABB1=A1B,得 平面A1BC,所以AD⊥BC。
平面A1BC,所以AD⊥BC。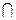 AD=A,从而BC⊥侧面A1ABB1,
AD=A,从而BC⊥侧面A1ABB1,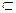 侧面A1ABB1,故AB⊥BC。
侧面A1ABB1,故AB⊥BC。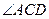 是直线AC与平面A1BC所成的角,
是直线AC与平面A1BC所成的角,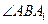 是二面角A1—BC—A的平面角,即
是二面角A1—BC—A的平面角,即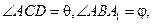
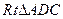 中,
中,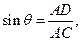 在
在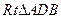 中,
中,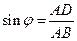 ,
,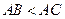 ,得
,得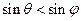 ,又
,又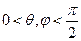 ,所以
,所以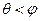 。
。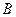 为坐标原点,以
为坐标原点,以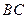 、
、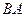 、
、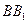 所在的直线分
所在的直线分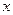 轴、
轴、 轴、
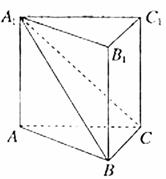
轴、 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,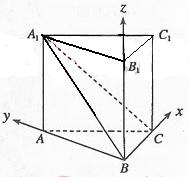
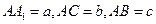 ,
,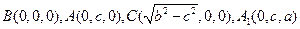 ,
,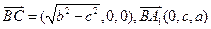 ,
,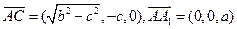 。
。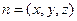 ,则
,则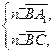 得
得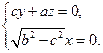
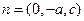 ,于是
,于是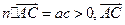 与
与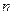 的夹角
的夹角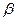 为锐角,则
为锐角,则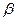 与
与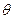 互为余角。
互为余角。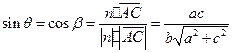 ,
,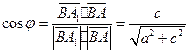 ,
,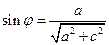 。
。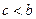 ,得
,得 ,
,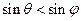 ,又
,又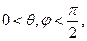 所以
所以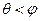 。
。

 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源:不详 题型:填空题
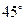 纬线上有A,B两点,设该纬线圈上A,B两点的劣弧长为
纬线上有A,B两点,设该纬线圈上A,B两点的劣弧长为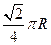 ,(R为地球半径),则A,B两点间的球面距离为__________________.
,(R为地球半径),则A,B两点间的球面距离为__________________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com