
分析 判断f(x)的奇偶性,单调性,值域,逐项判断.
解答 解:①∵f(-x)=-x-sin2x=-f(x),∴f(x)是奇函数,
∴f(x)的图象关于原点对称.故①正确;
②令g(x)=f(x)-3x=sin2x-2x,则g′(x)=2cos2x-2≤0,
∴g(x)是减函数,∵g(0)=0,
∴当x>0时,g(x)<0,即f(x)<3x.故②正确;
③当x→+∞时,f(x)→+∞,当x→-∞时,f(x)→-∞,
∴f(x)的值域为R,
∴不存在k∈R,使方程f(x)=k没有实数根,故③错误;
④∵数列{an}是公差为$\frac{π}{3}$的等差数列,
设a1=a2-$\frac{π}{3}$,a3=a2+$\frac{π}{3}$.
∴f(a1)+f(a2)+f(a3)=a2-$\frac{π}{3}$+sin(2a2-$\frac{2π}{3}$)+a2+sin2a2+a2+$\frac{π}{3}$+sin(2a2+$\frac{2π}{3}$)
=3a2-$\frac{1}{2}$sin2a2-$\frac{\sqrt{3}}{2}$cos2a2+sin2a2-$\frac{1}{2}$sin2a2+$\frac{\sqrt{3}}{2}cos$2a2
=3a2.
∵f(a1)+f(a2)+f(a3)=3π,∴3a2+2sina2=3π,∴a2=π.故④正确.
故答案为:①②④.
点评 本题考查了函数的性质判断,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
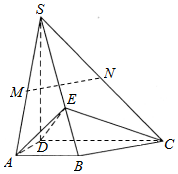 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,M,N分别为SA,SC的中点,E为棱SB上的一点,且SE=2EB.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,M,N分别为SA,SC的中点,E为棱SB上的一点,且SE=2EB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x2 | B. | f(x)=2x-1 | C. | f(x)=x2+cosx | D. | f(x)=xsinx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com