
【题目】二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
| … | 5 | 0 | -3 | -4 | -3 | m | … |
(1)m= ;
(2)在图中画出这个二次函数的图象;
(3)当![]() 时,x的取值范围是 ;
时,x的取值范围是 ;
(4)当![]() 时,y的取值范围是 .
时,y的取值范围是 .
【答案】(1)0;(2)图象见解析;(3)![]() 或
或![]() (4)
(4)![]() .
.
【解析】
(1)先确定出对称轴,根据抛物线的对称性即可求得;
(2)根据二次函数图象的画法作出图象即可;
(3)根据抛物线的对称性,(-4,5)关于直线x=-1的对称点是(2,5),根据图象即可求得结论,
(4)根据函数图象,写y的取值范围即可.
(1)由图表,根据抛物线的对称性,可知抛物线的顶点坐标为![]() ,
,
所以抛物线的对称轴的方程为![]() ,
,
又由![]() 关于直线
关于直线![]() 的对称点是
的对称点是![]() ,所以
,所以![]() .
.
(2)函数图象如图所示;
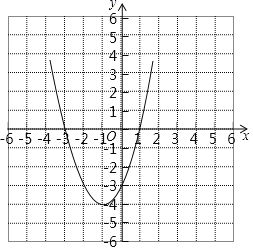
(3)因为![]() 关于直线x=-1的对称点是
关于直线x=-1的对称点是![]() ,
,
由图象可知当![]() 时,x的取值范围是
时,x的取值范围是![]() 或
或![]() ,
,
即x的取值范围是![]() 或
或![]() .
.
(4)由图表可知,当![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
结合图象可知当![]() 时,y的取值范围是
时,y的取值范围是![]() ,
,
即y的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.

根据该走势图,下列结论正确的是( )
A. 这半年中,网民对该关键词相关的信息关注度呈周期性变化
B. 这半年中,网民对该关键词相关的信息关注度不断减弱
C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D. 从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)抛物线的开口向 、对称轴为直线 、顶点坐标 ;
(2)当![]() 时,函数有最 值,是 ;
时,函数有最 值,是 ;
(3)当![]() 时,
时,![]() 随
随![]() 的增大而增大;当
的增大而增大;当![]() 时,
时,![]() 随
随![]() 的增大而减小;
的增大而减小;
(4)该函数图象可由![]() 的图象经过怎样的平移得到的?
的图象经过怎样的平移得到的?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种电路控制器在出厂时,每3件一等品应装成一箱,工人装箱时,不小心将2件二等品和1件一等品装入了一箱,为了找出该箱中的二等品,对该箱中的产品逐件进行测试,假设检测员不知道该箱产品中二等品的具体数量,求:
(1)仅测试2件就找到全部二等品的概率;
(2)测试的第2件产品是二等品的概率;
(3)到第3次才测试出全部二等品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“五四青年节”到来之际,启东中学将开展一系列的读书教育活动.为了解高二学生读书教育情况,决定采用分层抽样的方法从高二年级![]() 四个社团中随机抽取12名学生参加问卷调査.已知各社团人数统计如下:
四个社团中随机抽取12名学生参加问卷调査.已知各社团人数统计如下:
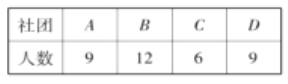
(1)若从参加问卷调查的12名学生中随机抽取2名,求这2名学生来自同一个社团的概率;
(2)在参加问卷调查的12名学生中,从来自![]() 三个社团的学生中随机抽取3名,用
三个社团的学生中随机抽取3名,用![]() 表示从
表示从![]() 社团抽得学生的人数,求
社团抽得学生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线y=x2+mx–2与x轴交于A,B两点,点C的坐标为(0,1).当m变化时,解答下列问题:
(1)能否出现AC⊥BC的情况?说明理由;
(2)证明过A,B,C三点的圆在y轴上截得的弦长为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com