
分析 (Ⅰ)利用零点分区间讨论去掉绝对值符号,化为分段函数,在每一个前提下去解不等式,每一步的解都要和前提条件找交集得出每一步的解,最后把每一步最后结果找并集得出不等式的解;
(Ⅱ)根据第一步所化出的分段函数求出函数f(x)的最小值,若?x0∈R,使得f(x0)+2m2<4m成立,只需4m-2m2>fmin(x),解出实数m的取值范围.
解答 解:(Ⅰ)当x<-2时,f(x)=|2x-1|-|x+2|=1-2x+x+2=-x+3,f(x)>3,即-x+3>3,解得x<0,
又x<-2,∴x<-2;
当$-2≤x≤\frac{1}{2}$时,f(x)=|2x-1|-|x+2|=1-2x-x-2=-3x-1,f(x)>3,即-3x-1>3,解得$x<-\frac{4}{3}$,又$-2≤x≤\frac{1}{2}$,∴$-2≤x<-\frac{4}{3}$;
当$x>\frac{1}{2}$时,f(x)=|2x-1|-|x+2|=2x-1-x-2=x-3,f(x)>3,即x-3>3,解得x>6,又$x>\frac{1}{2}$,∴x>6.
综上,不等式f(x)>3的解集为$({-∞,\;\;-\frac{4}{3}})∪(6,\;\;+∞)$.
(Ⅱ)f(x)=|2x-1|-|x+2|=$\left\{\begin{array}{l}{-x+3,x<-2}\\{-3x-1,-2≤x≤\frac{1}{2}}\\{x-3,x>\frac{1}{2}}\end{array}\right.$,
∴$f{(x)_{min}}=f({\frac{1}{2}})=-\frac{5}{2}$.
∵?x0∈R,使得$f({x_0})<4m-2{m^2}$,
∴$4m-2{m^2}>-\frac{5}{2}$,
整理得4m2-8m-5<0,
解得$-\frac{1}{2}<m<\frac{5}{2}$.
因此实数m的取值范围是$({-\frac{1}{2},\;\;\frac{5}{2}})$.
点评 本题考查了绝对值不等式的解法及分段函数的应用,分情况讨论去绝对值符号是关键,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
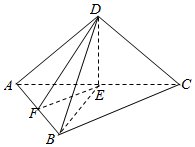 如图,在三棱锥D-ABC中,DA=DB=DC,D在底面ABC上的射影为E,AB⊥BC,DF⊥AB于F
如图,在三棱锥D-ABC中,DA=DB=DC,D在底面ABC上的射影为E,AB⊥BC,DF⊥AB于F查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线x=$\frac{5}{12}$π是函数f(x)的图象的一条对称轴 | |
| B. | 函数f(x)在[0,$\frac{π}{6}$]上单调递减 | |
| C. | 函数f(x)的图象向右平移$\frac{π}{6}$个单位可得到y=cos2x的图象 | |
| D. | 函数f(x)在[0,$\frac{π}{2}$]上的最小值为-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com