
分析 把(2+x)6 按照二项式定理展开可得,(1+x+x2)(2+x)6展开式中x2项的系数.
解答 解:把(2+x)6 按照二项式定理展开可得(2+x)6 =(${C}_{6}^{0}$•64+${C}_{6}^{1}$•32x+${C}_{6}^{2}$•16x2+…+${C}_{6}^{6}$•x6),
故(1+x+x2)(2+x)6=(1+x+x2)•(${C}_{6}^{0}$•64+${C}_{6}^{1}$•32x+${C}_{6}^{2}$•16x2+…+${C}_{6}^{6}$•x6),
故展开式中x2项的系数为16•${C}_{6}^{2}$+32${C}_{6}^{1}$+64=496,
故答案为:496.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于基础题


科目:高中数学 来源: 题型:选择题
| A. | ${A}_{5}^{2}$${A}_{2}^{2}$ | B. | ${A}_{7}^{7}$-${A}_{2}^{2}$${A}_{6}^{6}$ | ||
| C. | ${A}_{7}^{7}$-${A}_{6}^{6}$ | D. | ${C}_{10}^{8}$0.820.28 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
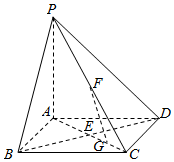 如图,四棱锥P-ABCD的底面是正方形,侧棱PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.
如图,四棱锥P-ABCD的底面是正方形,侧棱PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 20 | C. | 30 | D. | 42 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${(x-\frac{3}{2})^2}+{(y-\frac{3}{2})^2}=1$ | B. | ${(x-\frac{3}{2})^2}+{(y-\frac{3}{2})^2}=4$ | C. | (x-3)2+(y-3)2=1 | D. | (x-3)2+(y-3)2=2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com