
| A. | 命题”?x∈R,x2-x≤0”的否命题为”$?{x_0}∈R.x_0^2-{x_0}≥0$” | |
| B. | ”p∧q为真”是“p∨q为真”的必要不充分条件 | |
| C. | “若am2<bm2,则a<b”否命题为假 | |
| D. | 若实数x,y∈[-1,1],则x2+y2>1的概率为$\frac{π}{4}$ |
分析 A.根据否命题的定义进行判断,
B.根据复合命题真假关系进行判断,
C.根据否命题的定义 进行判断,
D.根据几何概型的概率公式进行判断.
解答 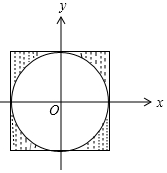 解:A.命题”?x∈R,x2-x≤0”的否命题为”?x0∈R,x02-x0>0,故A错误,
解:A.命题”?x∈R,x2-x≤0”的否命题为”?x0∈R,x02-x0>0,故A错误,
B.若p∧q为真,则p,q同时为真,则p∨q为真,则充分性成立,故B错误,
C.“若am2<bm2,则a<b”否命题为“若am2≥bm2,则a≥b”,则当m=0,a<b时,满足条件,但a≥b不成立,即否命题为假,故C正确,
D.x2+y2>1表示在圆的外部如图阴影部分,
则对应的概率为$\frac{2×2-π}{2×2}=\frac{4-π}{4}$=1-$\frac{π}{4}$,故D错误,
故选:C.
点评 本题以命题的真假判断与应用为载体,考查了几何概型,充要条件,四种命题,难度中档.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | A∩a=∅ | B. | a⊆A | C. | a∉A | D. | a∈A |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p:存在x∈R,x2+2x+2≤0;非p:当x2+2x+2>0时,x∈R | |
| B. | p:每一个四边形的四个顶点共圆;非p:存在一个四边形的四个顶点不共圆 | |
| C. | p:有的三角形为正三角形;非p:所有的三角形都不是正三角形 | |
| D. | p:能被3整除的整数是奇数;非p:存在一个能被3整除的整数不是奇数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 4 | C. | 5 | D. | -3或4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com