
分析 在①中,α内的直线与β相交、平行或包含于β;在②中,由面面垂直的性质得l⊥γ;在③中,由面面垂直的判定定理得α⊥γ;在④中,b与α相交、平行或b?α.
解答 解:在①中,如果α⊥β,那么α内的直线与β相交、平行或包含于β,故①错误;
在②中,如果α⊥γ,β⊥γ,α∩β=l,那么由面面垂直的性质得l⊥γ,故②正确;
在③中,若α∥β,β⊥γ,则由面面垂直的判定定理得α⊥γ,故③正确;
在④中,若α⊥β,α∩β=a,a⊥b,则b与α相交、平行或b?α,故④错误.
故答案为:②③.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:解答题
 如图在正方体ABCD-A1B1C1D1中,E是棱CC1的中点.
如图在正方体ABCD-A1B1C1D1中,E是棱CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
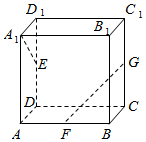 如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角的余弦值是0.
如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角的余弦值是0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
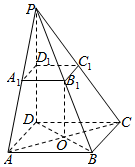 在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.
在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com