
分析 (1)数列{xn}满足x1=p+$\frac{1}{p}$,xn+1=${x}_{n}^{2}$-2.可得:x2=${x}_{1}^{2}$-2=${p}^{2}+\frac{1}{{p}^{2}}$.同理可得:x3=${p}^{4}+\frac{1}{{p}^{4}}$,x4=${p}^{8}+\frac{1}{{p}^{8}}$.
(2)猜想{xn}的通项公式为:xn=${p}^{{2}^{n-1}}$+$\frac{1}{{p}^{{2}^{n-1}}}$,利用数学归纳法证明即可.
(3)xn=${p}^{{2}^{n-1}}$+$\frac{1}{{p}^{{2}^{n-1}}}$,(n∈N*),0<p<1,可得xn>0,${p}^{{2}^{n-2}}$<$\frac{1}{{p}^{{2}^{n-2}}}$.可得xn+1-xn=${x}_{n}^{2}-{x}_{n}$-2=(xn-2)(xn+1),即可证明.
(4)利用数学归纳法证明即可.
解答 (1)解:∵数列{xn}满足x1=p+$\frac{1}{p}$,xn+1=${x}_{n}^{2}$-2.
∴x2=${x}_{1}^{2}$-2=$(p+\frac{1}{p})^{2}$-2=${p}^{2}+\frac{1}{{p}^{2}}$.
同理可得:x3=${p}^{4}+\frac{1}{{p}^{4}}$,x4=${p}^{8}+\frac{1}{{p}^{8}}$.
(2)解:猜想{xn}的通项公式为:xn=${p}^{{2}^{n-1}}$+$\frac{1}{{p}^{{2}^{n-1}}}$,
下面利用数学归纳法给出证明:
①当n=1时,x1=p+$\frac{1}{p}$,成立.
②假设当n=k(k∈N*)时成立,即xk=${p}^{{2}^{k-1}}$+$\frac{1}{{p}^{{2}^{k-1}}}$.
则xk+1=${x}_{k}^{2}$-2=$({p}^{{2}^{k-1}}+\frac{1}{{p}^{{2}^{k-1}}})^{2}$-2=${p}^{{2}^{k+1-1}}$+$\frac{1}{{p}^{{2}^{k+1-1}}}$,
因此当n=k=1时假设成立,.
综上可得:{xn}的通项公式为:xn=${p}^{{2}^{n-1}}$+$\frac{1}{{p}^{{2}^{n-1}}}$,(n∈N*).
(3)证明:∵xn=${p}^{{2}^{n-1}}$+$\frac{1}{{p}^{{2}^{n-1}}}$,(n∈N*),0<p<1,
∴xn>0,${p}^{{2}^{n-2}}$<$\frac{1}{{p}^{{2}^{n-2}}}$.
∴xn+1-xn=${x}_{n}^{2}-{x}_{n}$-2=(xn-2)(xn+1)=$({p}^{{2}^{n-2}}-\frac{1}{{p}^{{2}^{n-2}}})^{2}$(xn+1)>0,
∴xn+1>xn.
(4)证明:下面利用数学归纳法证明:$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{1}{x}_{2}}$+$\frac{1}{{x}_{1}{x}_{2}{x}_{3}}$+…+$\frac{1}{{x}_{1}{x}_{2}…{x}_{n}}$<p.0<p<1.
①n=1时,$\frac{1}{{x}_{1}}$=$\frac{1}{p+\frac{1}{p}}$<$\frac{1}{\frac{1}{p}}$=p.
②假设n=k(k∈N*)时:$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{1}{x}_{2}}$+$\frac{1}{{x}_{1}{x}_{2}{x}_{3}}$+…+$\frac{1}{{x}_{1}{x}_{2}•…•{x}_{k}}$<p,
∵xn+1>xn>0.
则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{1}{x}_{2}}$+$\frac{1}{{x}_{1}{x}_{2}{x}_{3}}$+…+$\frac{1}{{x}_{1}{x}_{2}•…•{x}_{k}}$+$\frac{1}{{x}_{1}{x}_{2}•…•{x}_{k+1}}$<$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{1}}$($\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{1}{x}_{2}}$+$\frac{1}{{x}_{1}{x}_{2}{x}_{3}}$+…+$\frac{1}{{x}_{1}{x}_{2}•…•{x}_{k}}$)<$\frac{1+p}{{x}_{1}}$=p,
因此n=k+1时也成立.
综上可得:$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{1}{x}_{2}}$+$\frac{1}{{x}_{1}{x}_{2}{x}_{3}}$+…+$\frac{1}{{x}_{1}{x}_{2}…{x}_{n}}$<p.
点评 本题考查了递推关系、乘法公式、数学归纳法、不等式的性质,考查了猜想归纳推理能力与计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{\begin{array}{l}3\end{array}}$ | B. | $\frac{2}{\begin{array}{l}3\end{array}}$ | C. | $\frac{1}{\begin{array}{l}4\end{array}}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
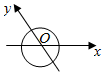 如图,Ox、Oy是平面内相交成120°的两条数轴,${\overrightarrow e_1}$,${\overrightarrow e_2}$分别是与x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x${\overrightarrow e_1}$+y${\overrightarrow e_2}$,则将有序实数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标.若$\overrightarrow{OP}$=(3,2),则|$\overrightarrow{OP}$|=$\sqrt{7}$.
如图,Ox、Oy是平面内相交成120°的两条数轴,${\overrightarrow e_1}$,${\overrightarrow e_2}$分别是与x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x${\overrightarrow e_1}$+y${\overrightarrow e_2}$,则将有序实数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标.若$\overrightarrow{OP}$=(3,2),则|$\overrightarrow{OP}$|=$\sqrt{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com