
分析 由条件利用函数y=Asin(ωx+φ)的图象变换规律可得所得函数的解析式,再利用正弦函数、余弦函数的奇偶性,可得 $\frac{π}{4}$+φ=kπ+$\frac{π}{2}$,k∈z,由此求得φ的取值.
解答 解:将函数y=sin(2x+φ)的图象沿x轴向左平移$\frac{π}{8}$个单位后,得到函数y=sin[2(x+$\frac{π}{8}$)+φ]=sin(2x+$\frac{π}{4}$+φ)的图象,
再根据y=sin(2x+$\frac{π}{4}$+φ)为偶函数,可得$\frac{π}{4}$+φ=kπ+$\frac{π}{2}$,k∈z,即$φ=\frac{π}{4}+kπ$,k∈z,
故答案为:φ=kπ+$\frac{π}{4}$,k∈z.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的奇偶性,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连接CB,并延长与直线PQ相交于点Q,若AQ=6,AC=5,则弦AB的长为$\frac{10}{3}$.
如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连接CB,并延长与直线PQ相交于点Q,若AQ=6,AC=5,则弦AB的长为$\frac{10}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若f′(x0)不存在,则曲线y=f(x)在点(x0,y0)处就没有切线 | |
| B. | 若曲线y=f(x)在点(x0,y0)处有切线,则f′(x0)必存在 | |
| C. | 若f′(x0)不存在,则曲线y=f(x)在点(x0,y0)处的切线斜率不存在 | |
| D. | 若曲线y=f(x)在点(x0,y0)处没有切线,则f′(x0)有可能存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 99 | B. | 100 | C. | 101 | D. | 102 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
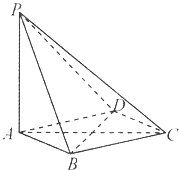 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一个不小于2 | B. | 都小于2 | ||
| C. | 至少有一个不大于2 | D. | 都大于2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com