
分析 利用函数的导数,求出导函数,通过导函数值的范围,求解倾斜角的范围.
解答 解:∵f(x)=$\frac{1}{2}$(x3-$\frac{1}{x}}$),
∴f′(x)=$\frac{1}{2}$(3x2+$\frac{1}{{x}^{2}}$)≥$\sqrt{3}$,
点P为函数f(x)=$\frac{1}{2}$(x3-$\frac{1}{x}}$)图象上任一点,则过点P的切线的斜率的范围:k≥$\sqrt{3}$.
过点P的切线的倾斜角为α,tanα≥$\sqrt{3}$.
过点P的切线的倾斜角取值范围:$[{\frac{π}{3},\frac{π}{2}})$.
故答案为$[{\frac{π}{3},\frac{π}{2}})$.
点评 本题考查直线的斜率与倾斜角的关系,函数的导数的应用,考查计算能力.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
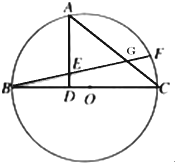 如图,BC是圆O的直径,点F在弧$\widehat{BC}$上,点A为弧$\widehat{BF}$的中点,作AD⊥BC于点D,BF与AD交于点E,BF与AC交于点G.
如图,BC是圆O的直径,点F在弧$\widehat{BC}$上,点A为弧$\widehat{BF}$的中点,作AD⊥BC于点D,BF与AD交于点E,BF与AC交于点G.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∧(¬q) | C. | (¬p)∧q | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±4x | B. | y=±2x | C. | y=±$\frac{1}{2}$x | D. | y=$\frac{1}{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | (-∞,4] | C. | [0,4] | D. | [0,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com