
分析 由条件利用两个向量垂直的性质,两个向量的数量积的定义求得cosθ的值,可得$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ的值.
解答 解:由题意可得($\overrightarrow{a}$-$\frac{5}{2}$$\overrightarrow{b}$)•($\overrightarrow{a}$+$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}$-$\frac{3}{2}$$\overrightarrow{a}•\overrightarrow{b}$-$\frac{5}{2}$${\overrightarrow{b}}^{2}$=4-$\frac{3}{2}$$\overrightarrow{a}•\overrightarrow{b}$-$\frac{5}{2}$=0,
解得$\overrightarrow{a}$•$\overrightarrow{b}$=1,∴2×1×cosθ=1,∴cosθ=$\frac{1}{2}$,求得θ=$\frac{π}{3}$,
故答案为:$\frac{π}{3}$.
点评 本题主要考查两个向量的数量积的定义,两个向量垂直的性质,属于基础题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
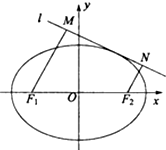 已知两点F1(-1,0),F2(1,0),点P在以F1,F2为焦点的椭圆C,且|PF1|,|F1F2|,|PF2|构成等差数列.
已知两点F1(-1,0),F2(1,0),点P在以F1,F2为焦点的椭圆C,且|PF1|,|F1F2|,|PF2|构成等差数列.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{1{3}^{2}}$-$\frac{{y}^{2}}{1{2}^{2}}$=1 | B. | $\frac{{x}^{2}}{1{3}^{2}}$-$\frac{{y}^{2}}{{5}^{2}}$=1 | ||
| C. | $\frac{{x}^{2}}{{3}^{2}}$-$\frac{{y}^{2}}{{4}^{2}}$=1 | D. | $\frac{{x}^{2}}{{4}^{2}}$-$\frac{{y}^{2}}{{3}^{2}}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
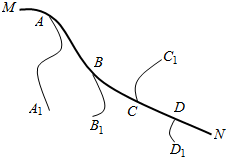
| A. | A处 | B. | D处 | ||
| C. | B、C间的任何一处(包括B、C) | D. | A、B之间的任何一处(包括A、B) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移1个单位 | B. | 向右平移1个单位 | C. | 向左平移2个单位 | D. | 向右平移2个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
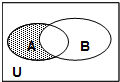 已知全集U=R,集合A={x|x>1},集合B={x|3x-4≤0},满足如图所示的阴影部分的集合是( )
已知全集U=R,集合A={x|x>1},集合B={x|3x-4≤0},满足如图所示的阴影部分的集合是( )| A. | {x|x>1} | B. | {x|1<x≤$\frac{4}{3}$} | C. | {x|x≤1} | D. | {x|x>$\frac{4}{3}$} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com